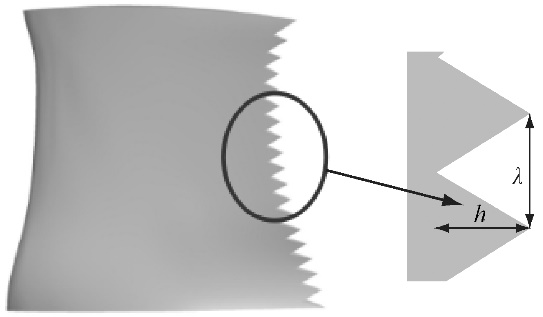
锯齿尾缘叶片对轴流风机气动噪声及性能的影响发表时间:2023-07-04 13:29 摘 要: 以OB-84型动叶可调轴流风机为研究对象,采用大涡模拟和FW-H声学模型对锯齿尾缘动叶风机进行了数值模拟,探讨了不同锯齿长度的尾缘对风机气动噪声、压强脉动及性能的影响,并分析了其流场特征和降噪机理。结果表明:锯齿尾缘可明显降低风机的中低频段噪声和流道中气流的压强脉动强度,锯齿长度越大,其影响越明显;锯齿尾缘增强了尾流区的流动掺混,改变了动叶尾缘脱落涡结构,形成了2层整齐的“梳状”流向对涡,由此降低了风机的气动噪声;模型A、模型B和模型C均可以在设计流量或小流量下提高风机效率,以模型A提升最明显,但在大流量下性能均低于原风机。 关键词: 噪声污染是泵、风机和压气机等旋转机械亟待解决的主要问题之一。目前,机械噪声可得到有效控制,而叶片旋转产生的气动噪声则成为主要噪声源。因此,降低旋转机械的气动噪声具有重要意义。 研究发现,猫头鹰具有的寂静飞行的本领来源于其翅膀尾缘独特的锯齿形结构。近年来,将仿生学概念应用于工程领域备受关注。理论研究中,Howe[1]通过分析猫头鹰翅膀的锯齿尾缘,建立了锯齿尾缘流场的声学模型,探究了锯齿尾缘降低噪声的可行性。Lilley[2]根据Lighthill气动声学理论,提出了锯齿尾缘机翼的远场噪声强度预测模型,但模型计算结果与实际测量结果有较大误差。Lyu等[3]建立了更精确的锯齿尾缘噪声分析模型,指出锯齿尺寸对降低远场噪声有重要影响。Huang[4]提出了一种用于预测锯齿尾缘平板对声波散射的理论模型,发现较大的锯齿长度和宽度可有效地降低散射波的强度,且长度的影响更为突出。Jones等[5]、黄乾[6]和仝帆等[7-8]基于数值模拟方法分析了锯齿尾缘的降噪机理,认为锯齿尾缘降低了翼型流场的压强脉动,使涡结构破碎更迅速,锯齿尾缘的降噪效果主要体现在中低音频段,但研究对象局限在展向截面相同的翼型上,流场相对简单。杨景茹等[9]采用大涡模拟方法探讨了锯齿尾缘翼型的气动特性,发现锯齿尾缘可推迟边界层分离,加速尾流掺混和能量扩散,但未说明这种流动特征与气动噪声的关系。 实验研究中,Gruber[10]通过在美国国家航空咨询委员会(NACA)翼型尾缘镶嵌锯齿来研究仿生结构的降噪效果,结果表明锯齿尾缘可降低噪声约5 dB。Chong等[11-13]研究了锯齿尾缘对翼型离散噪声的影响,发现锯齿尾缘可显著降低不稳定离散噪声。Vathylakis等[14]通过平板实验研究了锯齿尾缘的降噪机理,结果表明锯齿尾缘处的对流显著增大,锯齿后缘的功率谱密度和翼展方向相干性对降噪效果影响较小,锯齿两侧的倾斜壁面是降低噪声的关键。Ryi等[15]通过风洞实验测试了在风力机模型叶片尾缘分别加装直锯齿与倾斜锯齿对噪声的影响,发现两者均可降低噪声。陈坤等[16]根据猫头鹰羽毛的消声机理,将消声特征以条纹结构和锯齿的形式加装在小型风机叶片上,发现不同转速下的整机噪声均有不同程度的降低。Lee等[17]通过实验发现锯齿尾缘螺旋桨可降低噪声5.8 dB,但并未阐释降噪原因。郭晋之等[18]研究了锯齿对喷嘴的影响,发现锯齿形喷嘴可降低低频噪声,但增加了高频噪声。 综上所述,采用锯齿尾缘结构可有效降低气动噪声,但目前研究对象多为二维孤立翼型或平板,或风机结构相对简单,仍缺乏深入的机理分析。动叶可调轴流风机以其效率高和调节范围宽等优点而广泛应用于电站、煤矿和航空等领域,其内部结构更为复杂,不仅采用气动性能更好的三维扭叶片,而且通过布置导叶可进一步改善其气动噪声和性能,使得该类型风机的整体噪声和性能明显有别于结构相对简单的小型通风机。已有的锯齿尾缘降噪理论是否适用于大型轴流风机仍需进一步探讨,目前尚无这方面的研究报道,因此提高此类风机的气动性能并降低气动噪声具有更为显著的经济效益和环境效益。笔者以OB-84型动叶可调轴流风机为研究对象,分析锯齿尾缘叶片的降噪潜力及其对气动性能的影响,获得优选叶片改型方案,通过内流特征阐明其内在机理,为优化风机叶片结构、改善风机性能提供理论基础。 1 数值计算方法 1.1 几何模型 OB-84型动叶可调轴流风机由集流器、动叶区、静叶区和扩压器等组成。动叶和导叶数分别为14和15,动叶为三维弯扭叶片(如图1(a)所示),50%叶高处的弦长c=230 mm,转速为1 200 r/min,轮毂比为0.6,叶顶间隙为4.5 mm。在设计工况下,安装角为32°,入口处空气的体积流量为37.14 m3/s,全压为2 244 Pa,效率为83%[19]。 研究表明,猫头鹰翅膀的锯齿尾缘长度L为5~25 mm,宽度b为10~20 mm[20]。因锯齿长度对降噪效果起主要影响[3-5],故选取3种宽度相同(b=17 mm)但长度递增的锯齿结构。Avallone等[21]以壁面边界层厚度的整数倍取锯齿长度,得到了很好的降噪效果,故笔者以边界层厚度的2~4倍取L为14 mm、21 mm、28 mm,L/c为0.06、0.09、0.12。为便于描述,采用锯齿尾缘动叶的风机模型,按照L增大的顺序依次称为模型A、模型B和模型C。目前,有附加式和切割式2种生成锯齿尾缘的方法,笔者采用降噪效果更好的切割叶片的方法在动叶尾缘生成锯齿[13],如图1(b)所示。因原动叶为三维扭叶片,为保证锯齿延伸方向相同,个别锯齿尺寸略有差异。为优化计算资源,考虑到风机运行时的周期性特点,采用单流道风机模型,如图2所示,坐标轴x正向为主流方向。
(a) 原动叶
(b) 有锯齿尾缘的动叶 图1 三维动叶模型 Fig.1 3D model of a rotating blade
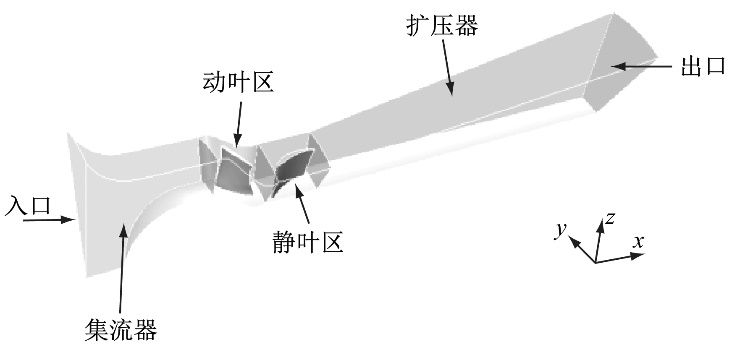
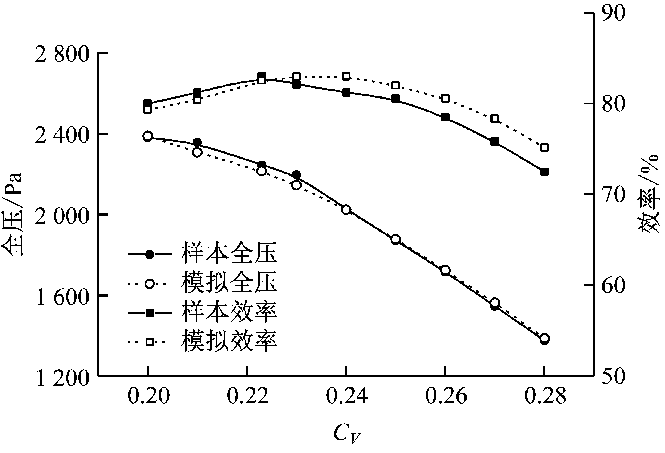
图2 单流道风机模型 Fig.2 Model of a single flow passage 1.2 控制方程及边界条件 数值模拟采用稳态求解方法,控制方程包括连续性方程、雷诺时均方程和更适于旋转流动、二次流与流动分离的Realizable 设置集流器入口为速度入口,扩压器出口为自由出口。进口截面处的湍动能和湍流耗散率根据入口速度和特征长度通过经验公式来确定[23]。使用多参考坐标系模型来解决动叶和机壳动静干涉,各区域交界面采用interface以实现参数的传递,整个计算域的侧面设置为周期性边界条件。 使用结构化/非结构化网格划分计算区域,在模型总网格数为191万、275万、492万和636万时进行了模拟。结果表明:当网格数为492万和636万时计算结果差距很小。为保障计算精度同时缩短计算时间,采用492万网格数方案,其中动叶区288万网格,静叶区137万网格。 定义流量系数CV为 CV=qV/(u2A) (1) 式中:qV为体积流量;u2为叶轮外圆周速度;A为动叶区流道截面积。设计工况下流量系数为0.223。 图3对比了模拟与样本值的性能曲线[24]。由图3可以看出,单流道模拟结果与样本值吻合良好,全压偏差小于2%,平均偏差小于1%;效率的最大偏差为3.9%,平均偏差为2%,由此保证了所建模型的可靠性。
图3 模拟值与样本值的对比 Fig.3 Comparison between simulated and experimental results 2 结果与分析 2.1 噪声频谱 将稳态计算结果导入大涡模拟中,取风机动叶转动1°的时间1.39×10-4
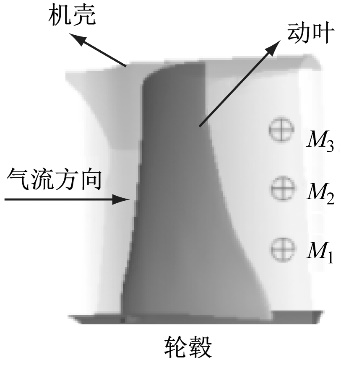
图4 监测点位置 Fig.4 Arrangement of monitoring points
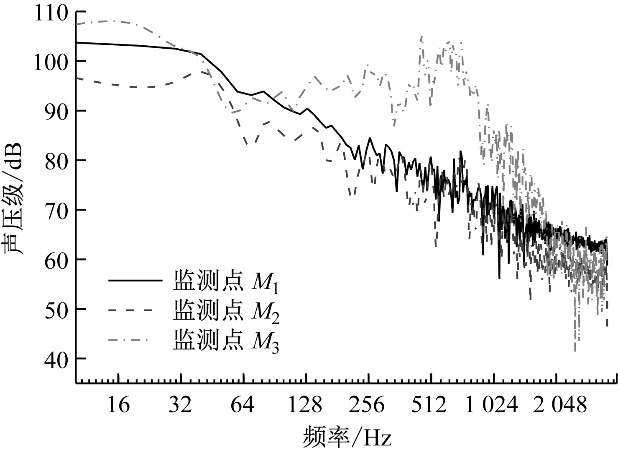
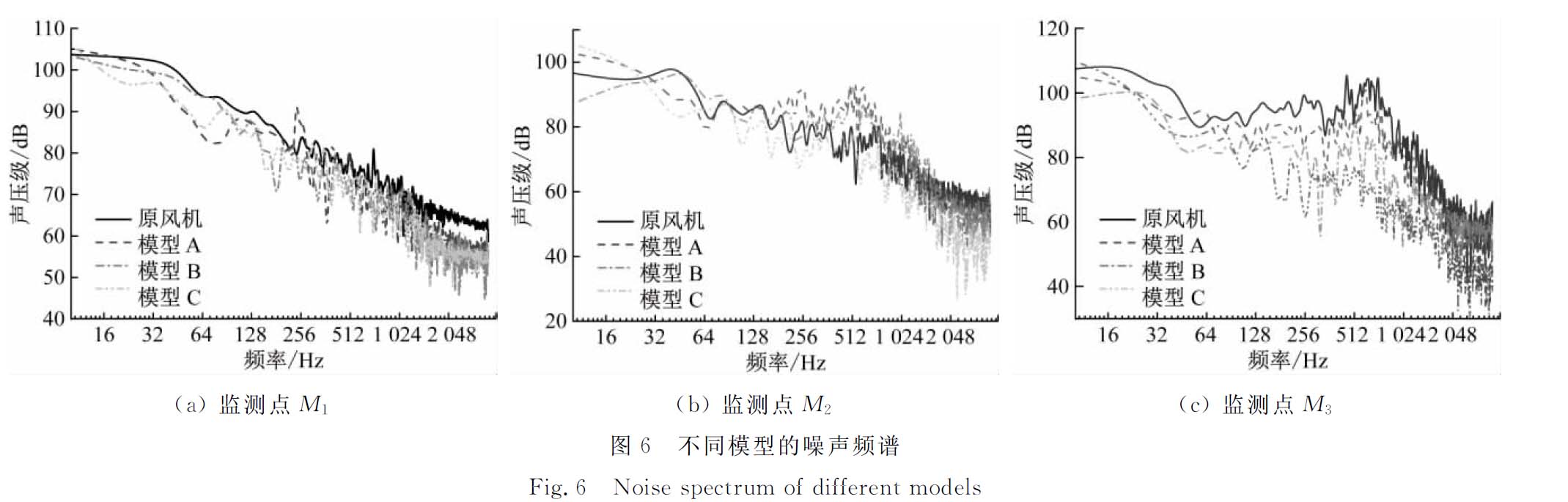
图5 原风机各监测点的噪声频谱图 Fig.5 Noise spectrum of each monitoring point for the original fan 为对比不同锯齿尾缘长度在各频段的降噪效果,图6给出了不同风机模型在各监测点的噪声频谱特征。由图6(a)表明,在监测点M1处,原风机位于频率10~20 Hz时噪声声压级最大为103 dB;当频率到达3 000 Hz后,声压级在63 dB处小幅波动。对于采用锯齿尾缘动叶的风机,高频段降噪效果相似,而当频率超过2 000 Hz后,噪声声压级最多降低9 dB;模型A和模型C在60 Hz时,气动噪声声压级远低于原风机;但在基频处模型A存在明显波峰,使得其在低频段的降噪效果不如模型C;各风机模型在中频段的噪声频谱差异不明显。 监测点M3靠近流道顶部位置,由图6(c)可知,模型A、模型B和模型C的监测点M3噪声声压级均低于原风机,尤其以模型B和模型C的噪声声压级下降最明显。4种风机模型在二倍频处均存在“驼峰”,原风机的“驼峰”最高点可达106 dB,随L增大,“驼峰”区逐渐缩小,在模型C中“驼峰”几乎完全消失,使得模型C的声压级在中频段最多可降低30 dB;在高频段,模型C的噪声也远低于其他模型,平均降噪约为11 dB。
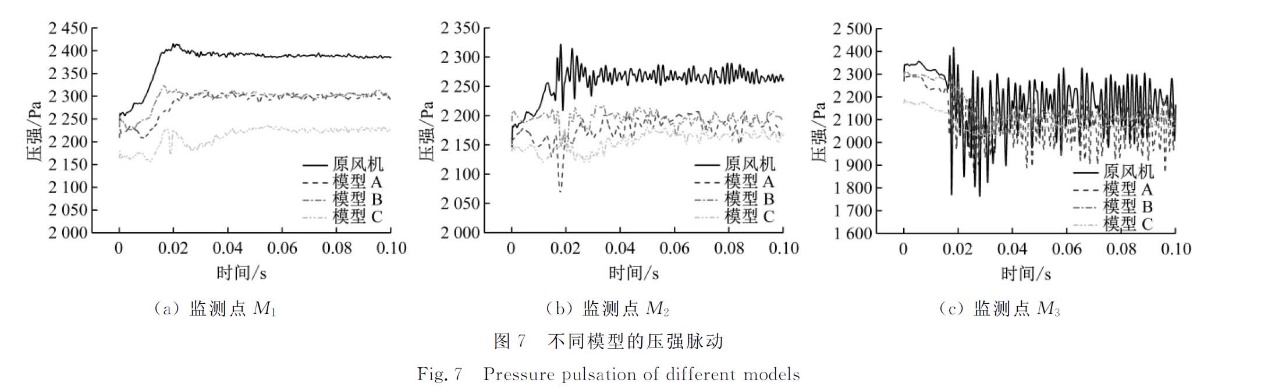
上述结果表明:模型A、模型B和模型C的气动噪声在全频段尤其是中低频段降低明显,且降噪效果与L呈正相关。Jones等[5]采用数值模拟方法进一步研究Grubur的实验时得到了相似的结论,即长锯齿尾缘翼型降噪效果更好。Lee等[17]在研究锯齿尾缘对螺旋桨的降噪效果时发现,其降噪效果在不同监测位置差距不大,这与文中所得不同位置监测点的噪声频谱差异较大的结果不同。其原因可能是,本研究中的动叶处于受限空间,流经动叶的气流受机壳、轮毂和静叶的影响,以及气流在各壁面间的相互干涉,由此造成动叶区不同位置噪声差异明显;而Lee等的研究对象处于大自由空间,故其降噪效果在空间分布上差异不大。 2.2 压强脉动 压强脉动是产生气动噪声的主要原因。图7给出了设计流量下风机在2个旋转周期内动叶区压强脉动的时域特性,监测点位置与前文一致。图7表明,4种风机模型在压强脉动振幅上存在明显差异。由图7(a)可知,在监测点M1,原风机压强曲线在0.02 s时存在一压强突增过程,这是因为将计算模型由稳态改为非稳态后,动叶产生的压强波动需要一段时间来传递到其后方的监测点所致。在0.04 s之后压强逐渐稳定在2 390 Pa,并保持小幅的周期性波动。模型A、模型B和模型C的压强脉动与原风机大致类似,但压强绝对值明显降低。由图7(b)可知,在50%叶高位置(监测点M2),模型A、模型B和模型C的压强绝对值同样低于原风机,但模型B和模型C的压强脉动振幅与原风机相比有小幅下降。由图7(c)表明,靠近叶顶位置处的压强脉动振幅显著增加,原风机在0.02 s前压强脉动振幅超过400 Pa,在0.04 s稳定在约180 Pa,部分位置达到300 Pa。模型A的压强脉动得到明显抑制,压强脉动振幅为150~200 Pa;L增大后,压强脉动振幅显著降低,其中模型B的压强脉动振幅约为30 Pa,而模型C的压强脉动振幅仅为5 Pa。
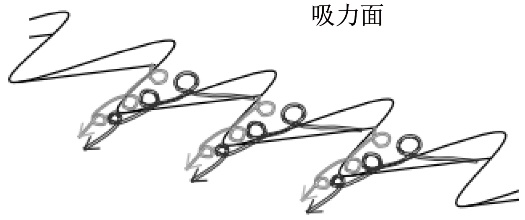
上述结果表明,锯齿尾缘可降低风机流道中的压强脉动强度,这与黄乾[6]对锯齿尾缘翼型流场模拟的结果相同,且随着L的增大,噪声抑制效果更加明显,这与前文的噪声频谱分析结果相互印证。 2.3 锯齿尾缘对涡结构的影响 Moreau等[25]通过实验研究了锯齿尾缘对平板的影响,指出尾缘噪声降低的主要原因是锯齿尾缘结构显著改善了尾流区流动。与其相比,文中的风机内部结构复杂,动叶和静叶排列较为紧密,且叶轮转速较高,因而风机动叶区与平板吹风实验的流场结构有本质区别。为揭示其降噪机理,图8给出4种风机模型的动叶表面和尾流的Q准则涡核分布。由图8可知,不同动叶的表面涡结构分布大致相同,即吸力面附着层状涡,从前缘一直延伸至弦长的3/4处;随后层状涡破碎消失,表明吸力面的边界层发展为湍流。图中涡结构的灰度代表叶片表面气流速度的大小,前缘顶部最高为117 m/s(区域A),尾缘中低部最低,不高于29 m/s(区域B)。
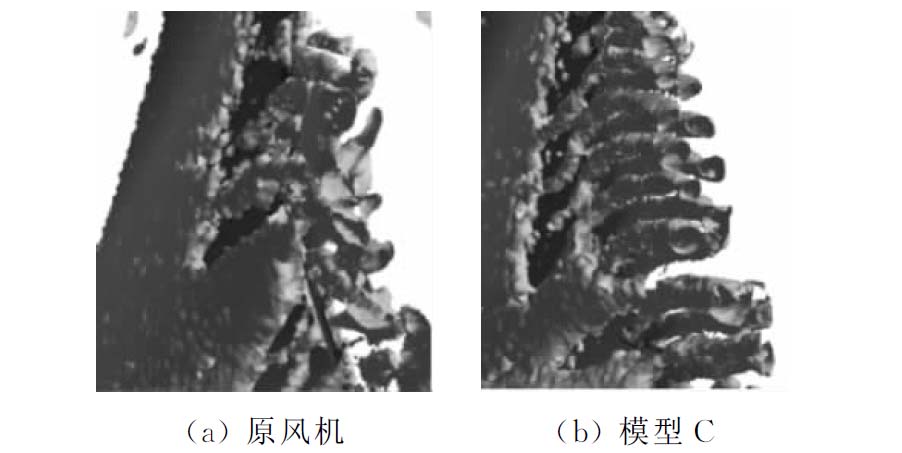
图8 不同模型的涡核分布 Fig.8 Vortex nucleus distribution of different models 对于原风机,动叶后衍生出不规则、条状且分布区域较大的脱落涡,其产生部位多数位于动叶尾缘后,少数产生于吸力面边界层。采用锯齿尾缘后,涡结构的瞬时速度基本保持不变,但展向涡结构分布不规则的现象得到改善:大尺寸涡破碎为小尺寸涡(区域I),且随着L加大,涡结构逐渐变细,分布更均匀,于锯齿处产生并沿流动方向延伸。模型C的脱落涡为细管状涡结构,形成整齐的“梳状”流向对涡(区域II),各涡之间伸展方向近似平行且相互独立,涡之间的距离近似保持一致,约为尾缘锯齿的齿宽。 图9给出了原风机和模型C的动叶尾缘脱落涡沿x轴负方向的局部放大图。由图9(a)可以看出,原风机中脱落涡的分布和大小较为随机,涡结构之间相互拥挤缠绕,延伸方向各不相同,多数在延伸时发生断裂。由图9(b)可以看出,采用锯齿尾缘后,流向对涡分布整齐,大小较为均匀,方向一致,涡结构之间相互分隔较为明显,保持得较为完整。
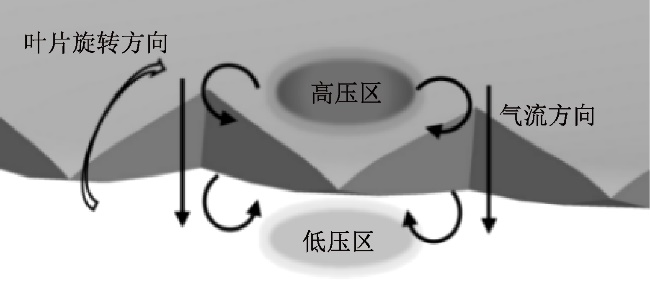
图9 尾缘脱落涡 Fig.9 Shedding vortex at trailing edge Chong等[12]提出了锯齿尾缘附近流向对涡假设(如图10所示),仝帆等[7]和杨景茹等[9]在模拟锯齿尾缘翼型的流场特征时验证了该假设,他们认为这是因吸/压强面之间存在压差,压强面侧的一部分气流从锯齿间隙流向吸力面,与吸力面气流掺混,从而在锯齿间隙生成流向对涡。图10的涡结构与图9(b)的涡结构有相似之处,但后者的尾缘涡呈双排分布,分别延伸于吸力面和压强面的齿根处,这表明此涡结构与已有研究中的锯齿尾缘涡有本质不同。由于文中的锯齿尾缘叶片处于高速旋转运动,动叶区气流受叶片推动,在锯齿的压强面形成高压区(见图11),吸力面形成低压区,同时一部分气流通过锯齿间隙提前从尾缘压强面到达吸力面。高压区两侧的气流受压差影响向锯齿间隙运动,形成了2个位置对称、旋转方向相反的对漩涡。同理,流过锯齿间隙的气流向低压区运动,在锯齿吸力面形成了2个对漩涡,且同一锯齿间隙的对漩涡旋转方向相同。
图10 流向对涡 Fig.10 Vortex pairs in flow direction
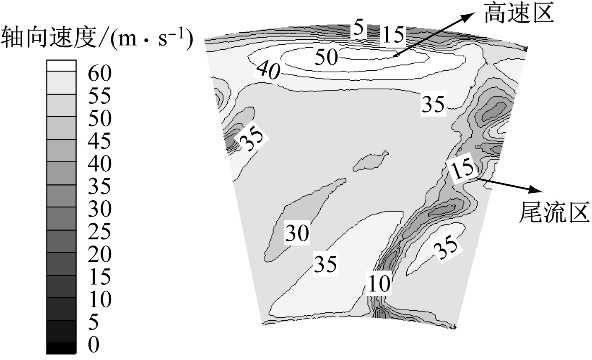
图11 对漩涡机理图 Fig.11 Mechanism diagram of vortex pairs 根据Powell的涡声理论,涡是产生流动噪声的根源,这种由锯齿尾缘诱发的流向对涡对减少单音节、单峰噪声起到积极影响[26]。同时,由于模型C的“梳状”流向对涡存在稳定性,使其在不同时刻的涡结构差异远小于原风机,这是前文锯齿尾缘降低风机流道压强脉动幅值的主要原因。 2.4 轴向分速度分布 由于模型C的降噪效果最明显,因此下文针对原风机和模型C开展内流特征分析。图12给出了原风机和模型C动叶区出口处截面的轴向速度分布(观察方向为沿x轴正向,风机逆时针旋转),可以反映动叶后流道的通流特征和尾流区特征。由图12(a)可知,由于轮毂和机壳附近的附面层较厚,轴向速度低至5 m/s。85%叶高中心处的轴向速度明显高于其他区域,最大可达50 m/s。这是因为在85%叶高处,叶片的周向速度大,气流所获机械能较多、通流能力较强。尾流区呈“峡谷”状从高速区右侧一直延伸至流道底部,此区域分布狭窄,并存在许多轴向分速度较低的漩涡,这说明流体流经叶片尾缘发生流动分离后,产生了分布较为扭曲且不均匀的尾缘涡。
(a) 原风机
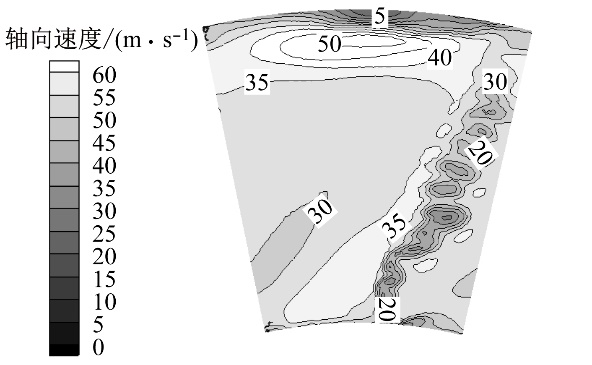
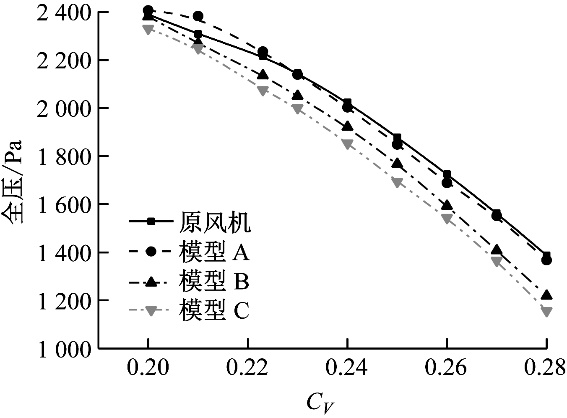
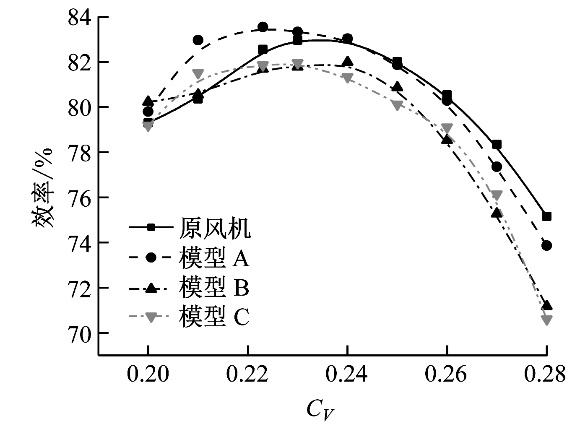
(b) 模型C 图12 流道的轴向速度分布 Fig.12 Axial velocity distribution in flow passage 采用锯齿结构的模型C(如图12(b)所示),其尾流区低速涡的数量增加、交替出现且排列更加整齐,最小速度增大至15 m/s;单个涡结构更加圆滑,相邻涡的面积差距不大,说明锯齿尾缘可以加速尾流区的流动掺混。上述特征与图9中的尾缘脱落涡分布基本一致。由图12可知,尾流区在流道中上部的分布范围最大,不同模型的尾流特征在此位置差异也更加明显,说明锯齿尾缘对流道内流特征的影响主要集中在流道中上部,这也是锯齿尾缘在流道中上部降噪效果更明显的原因。 2.5 风机性能 目前,有关锯齿尾缘对气动性能影响的研究仅集中在翼型的升力和阻力方面,其对流体机械性能的影响尚不明确,因此有必要进一步讨论。图13为原风机与模型A、模型B和模型C的全压和效率特性曲线。由图13可知,与原风机相比,模型A的全压在CV<0.22时有小幅提升,其余工况几乎相同;效率在CV=0.2~0.223时有明显提升,最高增加2.6个百分点,而在CV>0.27时降低2个百分点。模型B在大流量侧的全压和效率下降较为明显,分别平均下降107 Pa和1.2个百分点,但在CV=0.2时效率提高1.6个百分点。模型C的性能变化与模型B基本相同,全流量范围内全压和效率分别降低160 Pa和2个百分点,在CV=0.21时效率提高1.1个百分点。文献[14]、文献[27]和文献[28]中定性研究了锯齿尾缘翼型的气动性能,认为锯齿尾缘能够降低流动阻力,减少尾迹损失,这是在设计流量及小流量侧模型A、模型B和模型C效率提高的主要原因;但没有定量考虑由于切割尾缘使叶片面积减小所导致的气动损失,这种损失在大流量侧尤为明显。
(a) 全压特性曲线
(b) 效率特性曲线 图13 不同锯齿长度对风机性能的影响 Fig.13 Influence of serration length on the fan performance 上述结果表明,采用锯齿尾缘的动叶在小流量侧可提升风机效率,模型A提升最明显,高效区向小流量侧移动;而在大流量侧,锯齿风机的全压和效率均有不同程度降低,且锯齿尺寸越大,全压和效率下降越突出。鉴于风机在选型时工作参数裕量过大,导致风机运行工况多位于设计流量左侧,因此在实际工作时锯齿尾缘动叶对风机效率的影响不大,风机效率略有提升。 风机叶片改型要综合考虑降噪效果和经济效益:若风机多运行于设计流量及其左侧,模型C为优先方案,此时降噪收益最高且风机性能高于原风机;若风机多运行于大流量侧,则拥有一定降噪效果且性能与原风机最为接近的模型A为最优选择。 3 结 论 (1) 3种不同长度的锯齿尾缘均可明显降低风机的气动噪声,有效抑制噪声中频段“驼峰”现象的发生,降噪效果在全频段有效且主要集中在中低频段,降噪幅度与锯齿长度呈正相关。 (2) 风机动叶区的压强呈周期性变化,锯齿尾缘降低了风机流道中上部气流压强脉动的幅度,锯齿长度越大,抑制效果越明显。 (3) 锯齿尾缘改变了动叶尾缘脱落涡结构,将大尺寸涡破碎为小尺寸,形成2层整齐的“梳状”流向对涡,由此降低风机的气动噪声和压强脉动幅值;尾流区在流道中上部的分布范围最大,锯齿尾缘对气流的掺混作用在此处最明显,降噪和抑制压强脉动的幅度也最突出。 (4) 锯齿尾缘可在设计流量或小流量下提高风机效率,以模型A提升最明显;在大流量侧,模型A、模型B和模型C的性能均低于原风机,模型A的风机效率降幅最小;全工况下,模型B与模型C的性能差异不大。 参考文献: [1] HOWE M S. Noise produced by a sawtooth trailing edge[J]. [2] LILLEY G. A study of the silent flight of the owl[C]//4th [3] LYU B, AZARPEYVAND M, SINAYOKO S. Prediction of noise from serrated trailing edges[J]. [4] HUANG Xun. Theoretical model of acoustic scattering from a flat plate with serrations[J]. [5] JONES L E, SANDBERG R D. Acoustic and hydrodynamic analysis of the flow around an aerofoil with trailing-edge serrations[J]. [6] 黄乾. 基于大涡模拟的锯齿尾缘翼型流动分析及气动噪声预测[D]. 北京: 清华大学, 2015. [7] 仝帆, 乔渭阳, 王良锋, 等. 仿生学翼型尾缘锯齿降噪机理[J]. TONG Fan, QIAO Weiyang, WANG Liangfeng, et al. Noise reduction mechanism of bionic airfoil trailing edge serrations[J]. [8] 仝帆, 乔渭阳, 纪良, 等. 尾缘锯齿降低叶栅噪声的数值模拟[J]. TONG Fan, QIAO Weiyang, JI Liang, et al. Numerical simulation on noise reduction for the cascade with trailing edge serrations[J]. [9] 杨景茹, 杨爱玲, 陈二云, 等. 锯齿尾缘叶片气动特性和绕流流场的数值研究[J]. YANG Jingru, YANG Ailing, CHEN Eryun, et al. Numerical research on aerodynamic characteristics and flow fields of airfoil with serrated trailing edge[J]. [10] GRUBER M. Airfoil noise reduction by edge treatments[D]. Southampton,UK:University of Southampton, 2012. [11] CHONG T P, JOSEPH P F. An experimental study of airfoil instability tonal noise with trailing edge serrations[J]. [12] CHONG T P,JOSEPH P,VATHYLAKIS A,et al. On the noise and wake flow of an airfoil with broken and serrated trailing edges[C]//17th [13] CHONG T P, VATHYLAKIS A. On the aeroacoustic and flow structures developed on a flat plate with a serrated sawtooth trailing edge[J]. [14] VATHYLAKIS A, CHONG T P. On the turbulent boundary layers developed on flat plate with a serrated trailing edge[C]//19th [15] RYI J, CHOI J S. Noise reduction effect of airfoil and small-scale rotor using serration trailing edge in a wind tunnel test[J]. [16] 陈坤, 刘庆平, 廖庚华, 等. 利用雕鸮羽毛的消音特性降低小型轴流风机的气动噪声[J]. CHEN Kun, LIU Qingping, LIAO Genghua, et al. Aerodynamic noise reduction of small axial fan using hush characteristics of eagle owl feather[J]. [17] LEE H M, LU Z B, LIM K M, et al. Quieter propeller with serrated trailing edge[J]. [18] 郭晋之, 欧阳华, 田杰, 等. 锯齿形尾缘喷嘴气动声学实验及数值分析[J]. GUO Jinzhi, OUYANG Hua, TIAN Jie, et al. Analysis of aerodynamic acoustic characteristics of chevron nozzles[J]. [19] 索洛玛霍娃 T C. 通风机气动略图和特性曲线[M]. 陈富礼, 于绍和, 译. 北京: 煤炭工业出版社, 1986. [20] 陈坤. 三种鸮形态学、飞行运动学特征规律及其仿生研究[D]. 长春: 吉林大学, 2012. [21] AVALLONE F, van der VELDEN W C P, RAGNI D. Benefits of curved serrations on broadband trailing-edge noise reduction[J]. [22] 隽智辉, 王军, 唐俊, 等. 叶尖小翼安装位置对轴流风机性能的影响[J]. JUAN Zhihui, WANG Jun, TANG Jun, et al.Effects of tip end-plate installation position on the aerodynamic performance of an axial flow fan[J]. [23] 崔建光, 叶学民, 李春曦. 机匣处理对轴流风机性能影响的数值研究[J]. CUI Jianguang, YE Xuemin, LI Chunxi. Simulation of casing treatment effect on the performance of an axial flow fan[J]. [24] 李春曦, 尹攀, 叶学民. 变工况下动叶安装角异常对轴流风机气动和噪声特性的影响[J]. LI Chunxi, YIN Pan, YE Xuemin. Influence of abnormal blade installation angle on aerodynamic and acoustic characteristics of axial flow fan under variable working conditions[J]. [25] MOREAU D, DOOLAN C J. Tonal noise from trailing edge serrations at low Reynolds number[C]//19th [26] 孙晓峰, 周盛. 气动声学[M]. 北京: 国防工业出版社, 1994: 150-156. [27] LIU Xiao, AZARPEYVAND M, THEUNISSEN R. On the aerodynamic performance of serrated airfoils[C]//22nd [28] 武威. 锯齿尾缘叶片的气动性能研究[D]. 南京: 南京航空航天大学, 2016. 窗体顶端 窗体底端 Aeroacoustics YE (Key Lab of Condition Monitoring and Control for Power Plant Equipment, North China Electric Power University, Baoding 071003, Hebei Province, China) Abstract: Key 收稿日期:2019-05-08 修订日期:2019-07-10 基金项目:国家自然科学基金资助项目(11602085) 作者简介: 叶学民(1973-),男,河北邢台人,教授,博士,主要从事流体机械、流体动力学理论及应用方面的研究。 电话(Tel.):13932203443;E-mail:yexuemin@163.com。 文章编号:1674-7607(2020)03-0239-08 DOI:10.19805/j.cnki.jcspe.2020.03.010 中图分类号:TH4;O355 文献标志码:A 学科分类号:470.30 |