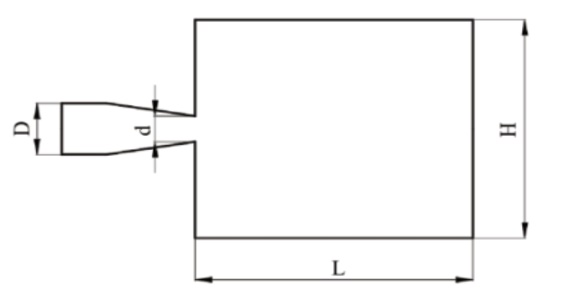
射流涡环喷嘴出口角度对涡环特性的影响

摘 要：空化射流喷嘴处理化工废水在近年来已成为相关热点研究问题，但传统射流技术相较于新型射流耦合应用存在一定局限性。涡环是自然界中常见的一种涡运动形态，对于整个湍流研究都具有重要意义，尽管涡环在自然界中比较容易产生，但真正应用于工程实际的涡环技术却比较少，因此将涡环技术及射流喷嘴相结合的喷嘴形式具有一定新颖及实用性。本文拟采用数值模拟的手段，对射流涡环喷嘴进行数值模拟分析，探讨了不同出口角度对涡环物理特征及传播特性的影响。

关键词：射流涡环喷嘴；出口角度；涡环；数值模拟

化工废水处理一直是环境治理问题的重中之重，空化射流处理化工废水的方式在近年来已成为一类热点问题，研究人员在此方面已设计出多种空化射流喷嘴，目前的研究仅关注于单一的水射流技术，未进一步扩展喷嘴形式及处理方式。涡环以其形态特殊、结构稳定、且具有出色的流体卷吸能力等特点，可将其应用在射流空化喷嘴上。通过研究发现^[1-3]，涡环射流相较于传统射流，其射流范围更大、扰动能力更强，因此研究一类新型射流涡环喷嘴对于废水处理领域具有一定实际意义。国内外有关射流涡环的研究大多对涡环自身结构特性开展研究，Maxworthy^[4]利用活塞装置产生涡环并初步研究了涡环的演化和生长的过程，发现涡环的形成时间会随入口直径的增大而增大，但未对出口结构及角度做进一步研究；向阳^[5]对涡环的物理特征开展了进一步研究，通过流函数的方法确定了涡环的边界，并探讨了有关涡环的运动学和动力学特性；陈昌隆^[6]则对涡环的的演化及涡环撞击固体壁面开展了相关研究，研究表明雷诺数会影响主涡环的诱导能力，雷诺数越高，则涡环的诱导能力越强。以上研究仅对涡环自身的特性开展了相关研究，未见有改变出口角度而对涡环所造成影响的研究。因此，本文模拟对射流涡环喷嘴开展研究，通过数值模拟的方法对不同出口角度下的涡环相关特性进行研究。

1.研究方法

本文采用仿真实验对简化的喷嘴出口射流的喷射过程、流场现象及尾涡环的发展变化进行了数值模拟，采用大涡模拟方法进行计算。

(1)计算方法和几何建模

为进一步对涡环喷嘴进行研究，建立了如图1所示的经简化的二维喷嘴射流轴对称几何模型，该模型是由一锥形喷嘴简化模型和水域组成，水域则简化成一个长方形。入口直径为D=5mm，出口直径为d，为表征出口角度的不同对射流涡环造成的影响，定义K=d/D，此后选用不同的K值进行计算，本文对K值的选用分别为0.2、0.3、0.4、0.5，入口速度设置为0.15m/s。为保证喷嘴喷射来流的均匀性以及考虑到射流尾迹区的尾流能够充分发展，再加消除边界对涡环形成的影响，在该计算模型中选取喷管出口半径为特征尺度，将整个长方形水域的长、宽尺寸确定为特征尺度的50倍、20倍，即取长方形水域的长和宽分别为62.5mm、25mm。

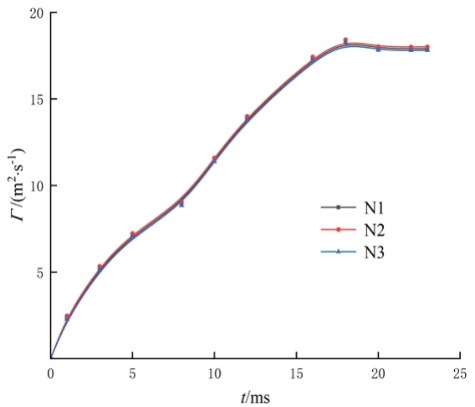
图1 简化喷嘴及外部流场模型

(2)无关性验证研究

为验证计算结果的准确性，需对计算模型进行网格无关性验证和结果准确性验证。

通过改变计算模型的网格数量来验证不同网格计算的准确性，选用涡环速度环量Γ进行验证，以此判断网格的收敛性。为简化处理，选用网格数量分别为105210、244649、407252。

由上述3组不同数量网格计算得到的Γ随时间变化如图2所示。由图2可见，三组网格计算的Γ都随着时间的变化而变化，曲线基本重合，仅N2的个别点有所偏移。为节省计算资源，选用较小的N1组进行后续计算。

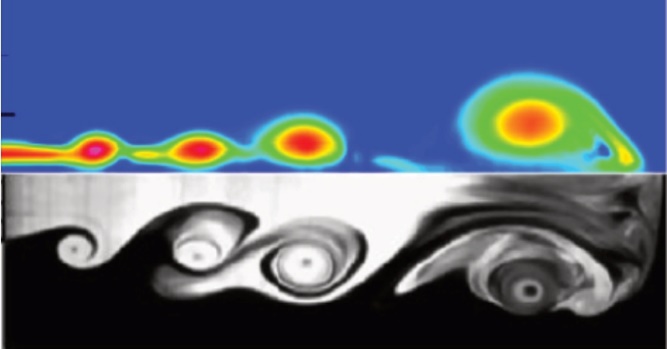
图2 不同网格条件下Γ随t的变化规律

为验证实验结果准确性，图3对比了相同条件下所模拟的射流涡环与Yu^[7]的涡量图。上方为模拟所得结果，下方为Yu通过实验所得。由图可见，二者的涡量图基本吻合，主涡环及尾涡的趋势具有一致性，因此本文所采用的计算方法准确性较高。

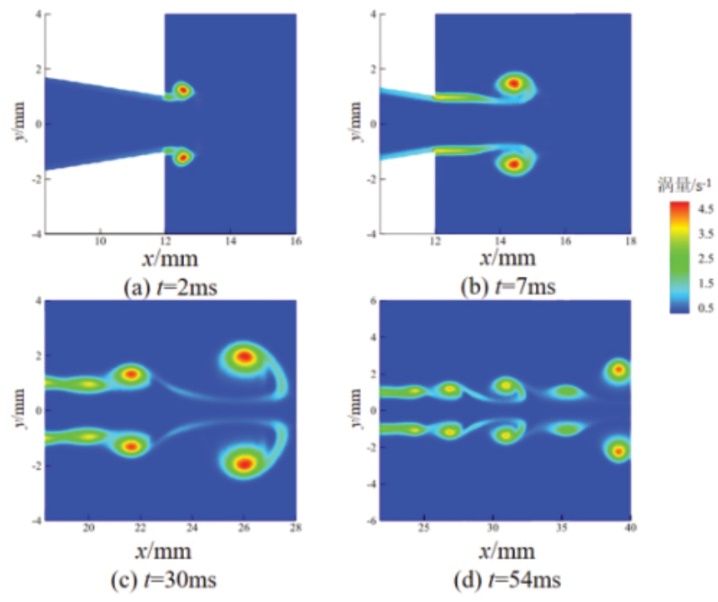
图3 实验结果涡量对比

2.结果与讨论

(1)涡环的形成及其演化过程

在射流离开喷嘴出口，向外界流动的同时，由于喷嘴出口处结构的影响，导致流体形成剪切层并进一步演化发展成涡环结构。此后，主涡环将进一步发展，不断地卷吸周围流体，将其吸入涡环内，直到达到其最大卷吸能力后，涡环则会达到夹止状态，此后涡环将不再继续生成，接下来卷吸的流体将在主涡环的诱导卷吸下形成尾迹涡环。此处以K=0.4为例，分析涡环的形成及演化过程，并将由于K值不同所造成的结果进行分析。

K=0.4时涡环的演化过程如图4所示。当t=2ms时，在出口附近的射流由于喷嘴出口的剪切作用，形成剪切层并开始卷起（见图4（a））；此后射流继续流动并卷起，在7ms时形成明显的涡核结构（见图4（b））；此后，涡环不断卷吸后方来流以及周围流体，涡环结构不断增大，直到达到最大卷吸能力，无法再吸收外界流体，而由于涡环的卷吸能力，其后所吸收的流体将以尾迹涡的形式出现在主涡环的尾部（见图4（c)）。当t=54ms时，主涡环将部分尾迹涡吸收，直到和尾迹涡分离（见图4（d））。在K=0.3、0.5的条件下涡环的发展趋势与K=0.4基本一致。而在K=0.2的条件下，情况则稍有变化。

图4 K=0.4时涡环发展涡量图

当K=0.2时，由于出口直径的缩小，涡环的形成与发展都要明显快于K=0.4的情况，主涡环仅在t=4ms左右便处于完全生长状态。此后在涡环不断发展的过程中，仅有主涡环所诱导的尾迹涡，而在喷嘴出口，仅产生了剪切层结构，但却未进一步发展为涡环结构。这主要是由于出口直径过小，出口处流速增大，剪切层形成时间过短而不足以产生涡环结构。

(2)出口角度对涡环重要参数的影响

本节主要分析出口角度与涡环的重要参数包括ω、r_c及r_r之间的关系。

①涡核内涡量分布

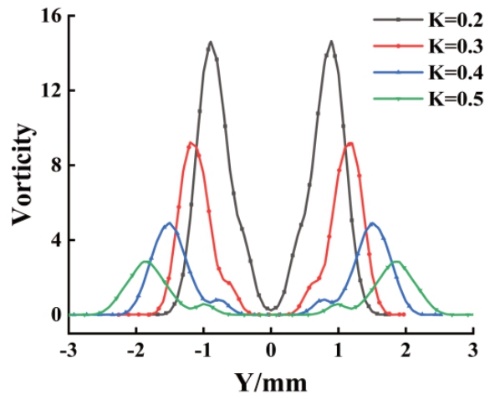
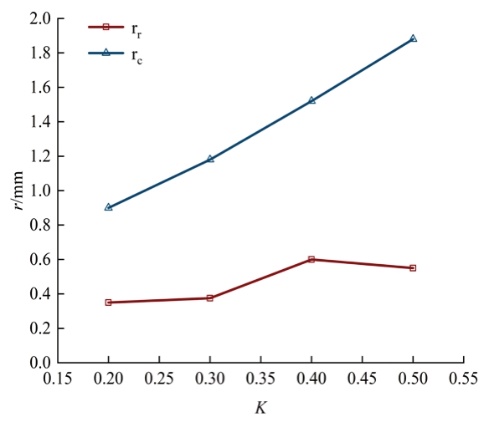
图5 不同K值涡量分布曲线对比

涡量可以显示出涡环对周围流体的卷吸情况，通过对四种条件下处于完全生长状态下的主涡环涡量进行对比，可以清晰地看出，不同K值下，涡环涡量的差距十分明显，其大小随K值的增大而不断减小。这主要是由涡量得计算方法和流体速度所导致得。一般来说，某点的涡量大小是流体微团绕该点旋转的平均角速度的两倍，也是流体速度矢量的旋度。由于K值越大，出口直径也越大，流体在出口的速度越小，这就导致了涡量的骤降。对于单个主涡环来说，涡环的卷吸能力往往比涡量的大小更为重要，通过实验发现，在K=0.4的条件下，主涡环的卷吸能力最佳。

②涡环半径和涡核半径

本文参考了Norbury^[8]对于涡环半径的分类，以此来界定涡环的直径及涡核直径。取涡量绝对值最大的两点间距离的一半定义为涡环半径（r_c），而涡核半径（r_r）则通过涡核速度分布的最大与最小值距离所确定。两半径随K值的变化如图6所示。由图可见，涡环半径rc的曲线增长趋势较为规律，基本与K值成正比。随着出口直径的不断增大，涡环在出口处所能够剪切成的涡环结构也就越大。而涡核半径的增长规律则稍有不同，可以看到，涡核直径的增长随着K值的增大并不规律。说明K值会对涡核的形成造成影响，而对涡环半径则无特殊影响。在K处于0.2至0.3之间，r_c反而减小，说明此时K对涡核的形成影响较大，而在K＞0.4后，r_c逐渐增大。因此可以认为，K对r_r、r_c的影响较大，尤其是对r_c影响较大，且四种条件下，K=0.4所产生的涡核增长速率最大。

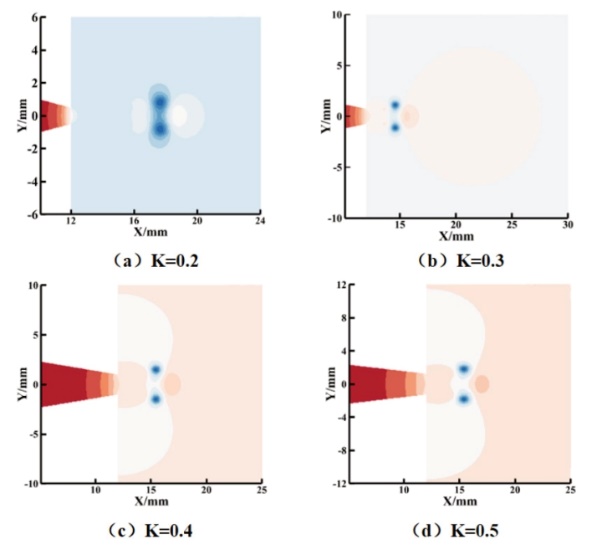
图6 r_c及r_r随K的变化情况

③涡环压力场变化

图7为涡环处于完全发展状态下的流场压力云图分布，由图可以看出，在4种K值条件下，涡核中心区域均出现了相对较大的负压区，其负压区位置与涡核中心区域基本重合，符合涡结构规律。其中，在K=0.4与K=0.5条件下，涡环的压力分布基本一致，均产生了弓形压力波，其产生的主要原因来自两方面：一方面是由于喷嘴出口的剪切层导致其出口处附近产生了较大压力，另一方面是由于涡环自身的连续卷吸特性，导致涡环前方压力增大并产生压力波，从而使得流体能够源源不断地被吸入涡环结构中。在K=0.2时，涡环已远离喷嘴出口，此时可见仅在主涡环前方存在较大的压力波动，而其后方的压力波则是由后方诱导卷吸形成的尾涡环的卷吸所造成的。因此可以认为，涡环由于自身卷吸特性，会使其前方产生压力波；该压力波的形成与涡核自身结构有关。涡核半径，即r_r越小，所产生的前方压力波也就越小；r_r越大，前方压力波也就越大。而涡环后方的压力波的来源主要有两种：一种是由后方诱导涡环的前方压力波所组合而成，称之为组合压力波；另一种是由喷嘴出口处的剪切层所贡献的，称之为剪切压力波。二者不会同时出现，其出现形式主要与涡环和喷嘴之间的距离所决定，经多组实验数据测定，一般当涡核与喷嘴出口之间的距离（L_c）与涡环直径（D_r）之比大于2时不会产生剪切压力波。

图7 不同K值下涡环压力云图对比

3.结论

本文结合数值模拟手段求解不同出口角度下喷嘴涡环的相关特性，计算结果与文献的相关实验结果相符合；分析不同出口角度下涡环的演化过程；给出了不同出口角度下涡环演变发展状态不同的解释；并分析了不同出口角度对涡环参数的重要影响，为进一步研究射流涡环喷嘴奠定了基础。研究主要得到以下结论：

（1）在入口条件一定的情况下，改变出口大小（K值）对涡环发展的影响较小，仅在K值小于0.2时，对尾迹涡的生成造成影响；

（2）在产生的涡环中，K=0.4时所产生的涡环涡量分布曲线斜率较大、涡量更为集中、涡核成长均匀、且结构更加稳定；

（3）相同条件下，K=0.4时涡核直径最大，对于同等工况下，选用K=0.4类型的喷嘴所产生的涡环影响范围更大。

【参考文献】

[1]Limbourg Raphaël.Formation of an orifice-generated vortex ring[J].Journal of Fluid Mechanics,2021,913(429):A29-A29.

[2]R.V.Akinshin.New Instability of a Thin Vortex Ring in an Ideal Fluid[J].Fluid Dynamics,2020,55(1):74-88.

[3]VLin,Shu jia,et al.Evolution of the Lagrangian drift and vortex added-mass of a growing vortex ring[J].Journal of Hydrodynamics,2021:1-11.

[4]T.Maxworthy.Some experimental studies of vortex rings[J].J.Fluid Mech,1977(80):465-495.

[5]向阳,刘洪,吴镇远.涡环物理特征的研究[J].空气动力学学报,2014,32(02):159-165.

[6]陈昌隆.合成射流涡环演化及其撞击固体壁面的试验研究[D].哈尔滨工业大学,2021.

[7]M.Yu,S.C.Vortex Formation Process of a Starting Square Jet[J].Aiaa Journal,46(01):223-231.

[8]Norbury J.A family of steady vortex rings[J].Journal of Fluid Mechanics,1972,57(03):417-431.

窗体顶端

窗体底端

lnfluence of Nozzle Exit Angle on Vortex Ring Characteristics

Li Wenyi,Li Qin^*,Huo Yingda,Xiao Fengkun(School of Chemical Equipment,Shenyang University of Technology,Liaoning,111000)

Abstract：In recent years,the treatment of chemical wastewater by cavitating jet nozzles has become a hot research topic,but the traditional jet technology has some limitations compared with the new jet coupling application.Vortex ring is a common form of vortex movement in nature,which is of great significance for the whole turbulence research.Although vortex ring is relatively easy to produce in nature,there are few vortex ring technologies that are really applied to engineering practice.Therefore,the nozzle form combining vortex ring technology with jet nozzle has certain novelty and practicality.In this paper,numerical simulation is used to analyze the jet vortex ring nozzle,and the effects of different outlet angles on the physical characteristics and propagation characteristics of the vortex ring are discussed.

Key words：jet vortex ring nozzle；exit angle；vortex ring；numerical simulation

中图分类号：TK221

文献标识码：A

【作者简介】李文溢（1997-），男，硕士，沈阳工业大学化工装备学院；研究方向：环保设备工程。

【通信作者】李勤（1965-），女，博士，教授，沈阳工业大学化工装备学院；研究方向：流体机械设计理论与应用。