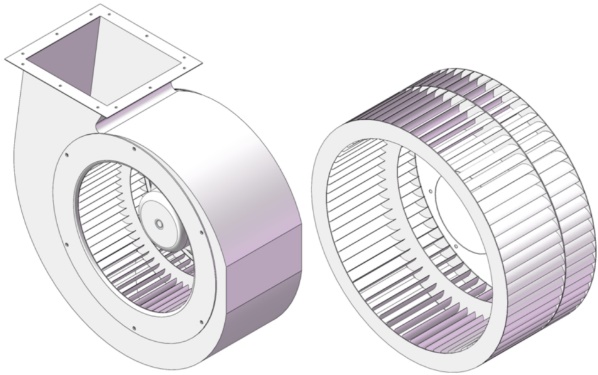
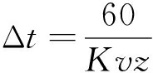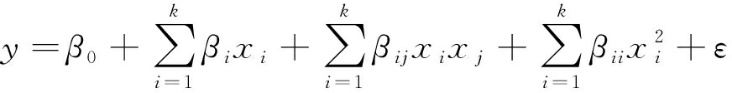多翼离心风机双圆弧叶片的参数优化设计及气动性能分析发表时间:2023-07-04 13:23 摘要:为改善多翼离心风机气动性能和噪声特性,结合双圆弧叶片具有较高流道设计自由度的特点,本文以性能较优的单圆弧叶片多翼离心风机为基础,通过CFD与实验相结合的方法对双圆弧叶片进行全参数匹配优化设计。以0 Pa静压工况下风机风量为优化目标,采用Box-Behnken响应面实验设计方法对双圆弧叶片的进口角、出口角、内外径比、拱点圆直径以及中心角进行参数方案设计,获得了46组样本空间。通过对设计参数和样本结果进行二次回归拟合,得到了双圆弧叶片参数与风量的函数关系及最优参数组合。结果表明,进口角和出口角在所有主效应中对风量的影响灵敏度最高,而进口角-出口角以及内外径比-中心角在所有交互效应中对风量的影响灵敏度最高。通过CFD和FW-H声类比方法对风机的气动性能和声场进行数值计算,计算结果表明优化风机的风量较原型风机增加了118 m3·h-1,相对提升9.7%。优化叶片能够有效抑制叶间流道内旋涡流的生成和发展,叶片的进、出口角与气流的进、出口流动冲角吻合度更高,有效减小了叶片前缘气流冲击产生的压力脉动以及尾迹流与蜗壳的非定常相互作用。实验结果表明,优化风机功率较原型机降低了4.7%,噪声下降了1.8 dB。 关键词:多翼离心风机;双圆弧叶片;Box-Behnken响应面法;参数化设计;气动性能 多翼离心风机具有结构紧凑、噪声低以及流量和压力系数高的优点,在空调器、吸油烟机等家用电器中得到广泛应用[1],同时随着生活水平的不断提高和对国家低碳生活的倡导,使得研究者对多翼离心风机气动性能的提升和噪声的控制技术的研究日益关注。叶轮作为多翼离心风机的主要做功部件,对多翼离心风机气动性能和噪声的影响是重要的。目前,对多翼离心风机叶轮的改进主要集中在叶片进口角β1、出口角β2、叶片型线、内外径比D1/D2和叶片数[2-3],以及采用叶片斜切[4-5]、仿鱼形叶片[6]、仿鸮翼叶片[7]和叶片前尾缘锯齿叶片[8]等,这些改进方式大多为单一参数或单一结构改进,很少涉及到多参数的协同匹配优化。目前多翼离心风机叶片中弧线大多为采用单圆弧型线,其设计参数较少,叶间流道的设计自由度较低。何立博等通过正交实验设计方法得到了单圆弧叶片的相对最优的参数水平组合,并通过试验验证了正交方法设计结果在实际产品性能上的提升[9]。李云龙等通过响应面方法对多翼离心风机的单圆弧叶片进行了优化设计,优化后风机的气动性能改善显著[10]。肖千豪采用最优拉丁超立方设计方法对单圆弧叶片进行了参数优化,优化后风机在多个工况下的风量和效率均得到提升[11]。王湛对双圆弧叶片在不同的圆弧曲率、圆心角以及进口角3个参数相互组合方式下的风机性能进行了研究,分析表明双圆弧叶片的气动性能要优于单圆弧叶片,但其并没有获得相对最优的双圆弧叶片参数组合以及各参数对风机性能的影响权重[12]。王珂等采用均匀设计方法对双圆弧叶片的进、出口安装角两个参数进行优化,改善了叶道内的流动分离现象,提高了风机的效率[13]。这些方法的应用为风机叶轮的优化提供了新的途径,有利于圆弧形叶片型线参数的改进,提升了叶轮性能。 上述研究对多翼离心风机叶片的设计具有重要意义,然而对双圆弧叶片型线的优化仅限于单个或少数几个参数的改进,未能考虑双圆弧叶片所有参数及其参数组合对风机性能的影响。双圆弧叶片与单圆弧叶片相比,可以更加自由地控制中心角和拱度。这使得流道形状的设计自由度提升,从而得到更合理的流道,但是双圆弧叶片的设计参数较多,并且参数之间交互作用较大,常规的优化方法很难协同匹配出最优的叶片参数组合。考虑到Box-Behnken响应面法(RSM)在多元线性回归的基础上可以寻找目标参数与各影响因子间的定量规律,获得各影响因子水平的最佳组合[14],鉴于此,本研究以某单圆弧叶片多翼离心风机为原型,在保持蜗壳参数不变的基础上,采用Box-Behnken响应面法对双圆弧叶片的叶片进口角、叶片出口角、叶轮内外径比、拱点圆直径Dc以及叶片中心角θ进行多参数协同优化设计,确定双圆弧叶片参数及其交互作用与风机风量之间的影响关系,得到双圆弧叶片的最优参数水平组合,以此提高风机的气动性能,改善风机内部流动状态。通过借助计算流体动力学(CFD)与样机实验结合的方法对最优参数组合实例进行进一步研究,验证该方法的有效性。 1 数值计算与原型机实验 1.1 几何模型及网格划分 图1为本文所研究的双吸多翼离心风机,其主要由集流器、蜗壳以及双吸叶轮组成。集流器和蜗壳是固定通流部件,叶轮是旋转部件,也是主要的做功部件。叶轮形式为双吸叶轮,中间由中盘进行间隔。叶片为等厚金属前向叶片,叶片数为60,叶片中弧线为单圆弧型线。单圆弧叶片的主要结构参数和本文原始风机单圆弧叶片所对应的结构参数分别如图2和表1所示。原始风机在最大流量工况点的转速为813 r·min-1,试验风量为1 218 m3·h-1。
(a)集流器、蜗壳 (b)叶轮图1 单圆弧叶片多翼离心风机Fig.1 Single-arc blade multi-blade centrifugal fan
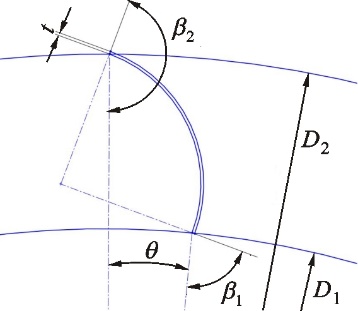
图2 单圆弧叶片主要结构参数Fig.2 Main structural parameters of single-arc blade 表1 原始单圆弧叶轮结构参数 Table 1 Original single-arc blade impeller structural parameters
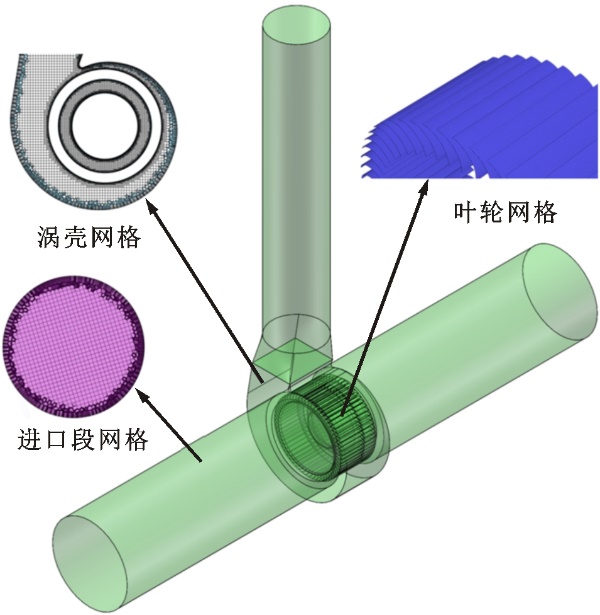
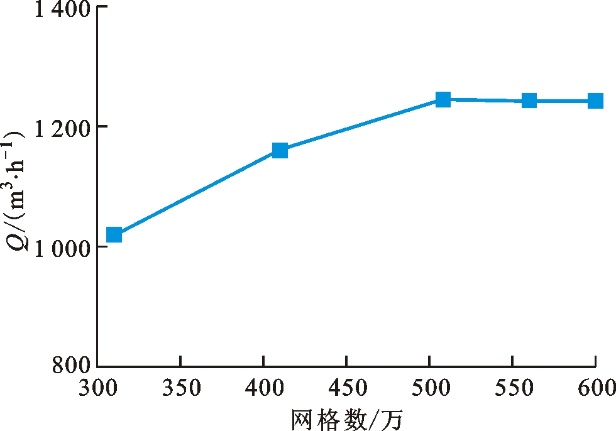
采用商业软件Creo 6.0对风机内流空气域进行建模,将整个计算域模型分为前后进口延伸段、出口延伸段、叶轮区域以及蜗壳区域。计算域网格采用fluent meshing进行划分,进出口域和蜗壳区域的网格采用多面体和六面体混合网格,叶轮区域采用结构化网格,对流域的近壁面进行局部加密并添加边界层,使近壁面的第一层网格y+处于30~100之间。计算域几何模型及各部分网格如图3所示。 以风机风量Q作为验证目标,对原始风机计算域的网格数进行网格无关性验证,总网格数与风机风量的关系如图4所示,在网格数为507万时,风量基本不再随着网格数的增加而变化,风量波动在0.25%的范围内。为了保证计算的准确性并减小计算时间,流体域的总网格数为507万,蜗壳和叶轮区域的网格数分别为166万和273万。
图3 风机流体域及各区域网格Fig.3 Fan fluid domain and grid of each domain
图4 网格无关性验证Fig.4 Grid independence verification 1.2 数值计算方法 采用计算流体力学软件ANSYS FLUENT 20.0对三维雷诺时均Navier-Stokes方程进行数值求解,计算风机的性能参数和内部流场。由于风机流动马赫数小于0.3,流动为不可压缩流动,湍流模型采用标准k-ε两方程模型,压力速度耦合求解采用SIMPLE算法,压力离散格式采用PRESTO!。流动控制方程的数值离散中,能量方程、动量方程和湍流耗散方程均采用二阶迎风格式。叶轮为旋转区域,采用Frame-motion模型,其他区域为静止区域,额定工况叶轮转速为813 r·min-1。 以定常计算得到的收敛解作为初始流场进行非定常流动计算。叶轮域采用Mesh-motion模型,差分格式使用二阶精度,时间步长根据下式确定
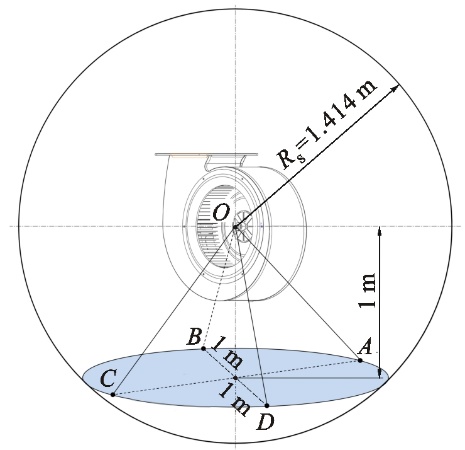
(1) 式中:K=40为单个时间步内的最大迭代次数;v为叶轮转速;z=60为叶片数。因此,非定常计算时间步长取3.125×10-5 噪声计算以非定常流动稳定后的结果作为FW-H声学方程的输入项,来求解声源区域远场噪声的声压级及声压脉动时均值等声场信息。噪声接收点根据GB/T 2888—2008《风机和罗茨鼓风机噪声测量方法》布置。噪声源选择为叶轮和蜗壳等壁面,测量方法为全球包络法,测量面为半球面,球半径为1.414 m,风机位于球心处,测量点均匀分布于被测风机中心以下1 m的水平面与球面相交的圆周上,如图5所示。根据计算模型位置,4个接收点的坐标分别为A(0 m,-1 m,-1 m)、B(1 m,-1 m,0 m)、C(0 m,-1 m,1 m)、D(-1 m,-1 m,0 m)。
图5 噪声测点分布Fig.5 Distribution of noise measuring points 1.3 试验测试 风机的气动性能测试按照GB/T1236—2017《工业通风机用标准化风道性能试验》进行。气动性能试验装置主要由被测风机、整流器、喷嘴以及数据采集系统等部分组成,其测量原理基于伯努利原理,通过变换出口挡板直径的大小,数据采集系统处理得到风机各个工况点风压、风量数据。为保证测试精度,风机测试前需热机0.5 h。图6为本文中本研究的原型多翼离心风机气动性能测试场景。 噪声测试在专业半消音室中进行,测试方法与图5中的噪声测试要求相同。噪声测量结果为A声压级在4个测点噪声的算术平均值。风机的噪声测试场景如图7所示。
图6 气动性能测试 图7 噪音测试Fig.6 Aerodynamic performance test Fig.7 Noise test 2 双圆弧叶片响应面优化设计 响应面优化法(RSM)是数学和统计学的结合,通过对受到多个因子影响的响应(设计目标)建立经验模型,得到响应与因子的关系,然后寻找优化区域,找到响应的优化值和对应的影响因子值[14],其过程包括筛选试验、试验设计、方程回归、回归方程检验和优化求解。由于响应和因子的真实函数关系未知且响应和因子之间存在非线性关系,响应函数常用多元二次多项式拟合,表达式如下
(2) 式中:y为响应;β0表示常数项;βi表示因子xi的线性效应;βij表示因子xi和因子xj之间的线性交互效应;βii表示因子xi的二次效应;ε为随机误差项。 通过对获得的回归方程进行显著性检验、回归系数显著性检验和失拟性检验来判断方程的合理性。经过检验后的方程可用于预测优化双圆弧叶片型线,通过极值存在条件以及绘制响应曲面图来计算最佳响应值。考虑到Box-Behnken设计试验次数少、效率较高的优点[14],本研究中的双圆弧叶片RSM设计采用Box-Behnken方法。
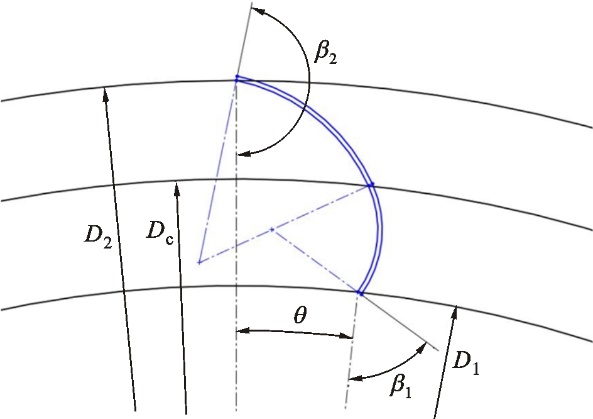
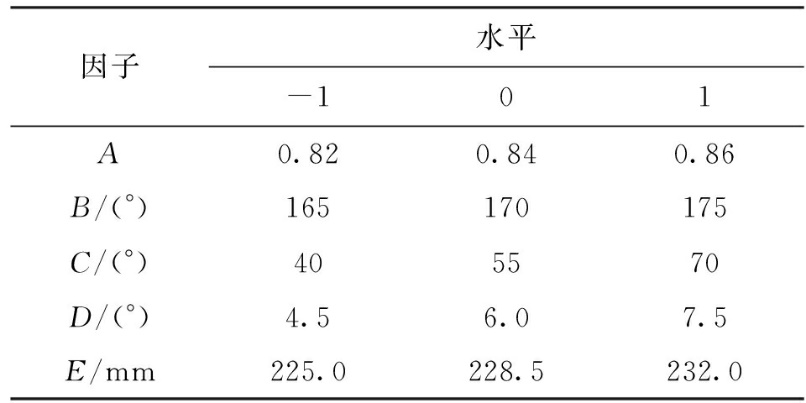
图8 双圆弧叶片型线相关设计参数Fig.8 Design parameters related to double-arc blade 2.1 Box-Behnken响应面试验设计 等厚叶片气动性能好坏主要由其叶片中弧型线所决定。与单圆弧叶片中弧线相比,双圆弧叶片型线参数更多,叶片设计难度也相应增加,但双圆弧叶片在设计时可以更加自由地控制叶片中心角和圆弧拱度,使得叶间流道形状的设计自由度提升,叶间流道形状更加符合气流在多翼离心风机内的流动特性。在变工况的条件下,双圆弧叶片的风量衰减比单圆弧叶片低。在保持蜗壳不变的基础上,研究双圆弧叶片型线的各参数及参数交互作用对风机性能的影响并获得最优叶片型线参数组合,选择双圆弧叶片型线的全部参数进行Box-Behnken响应面优化设计。研究采用Design Expert软件,根据相应实验设计方案,选择叶轮内外径比(因子A)、叶片进口角(因子B)、叶片出口角(因子C)、叶片中心角(因子D)以及拱点圆直径(因子E)5个参数作为影响因子,以风机0 Pa出口静压工况下的风量作为响应,研究双圆弧叶片型线各参数对风机气动性能的影响,双圆弧叶片的参数因子如图8所示。根据实际工程设计经验,设计因子的取值范围为D1/D2=0.82~0.87,β1=40°~70°,β2=165°~175°,θ=4.5°~7.5°,Dc=225~232 mm。为简化计算,将自然变量的因子转化为编码变量,因子及其水平见表2。 表2 双圆弧叶片影响因子及水平 Table 2 Influencing factors and levels of double-arc blade
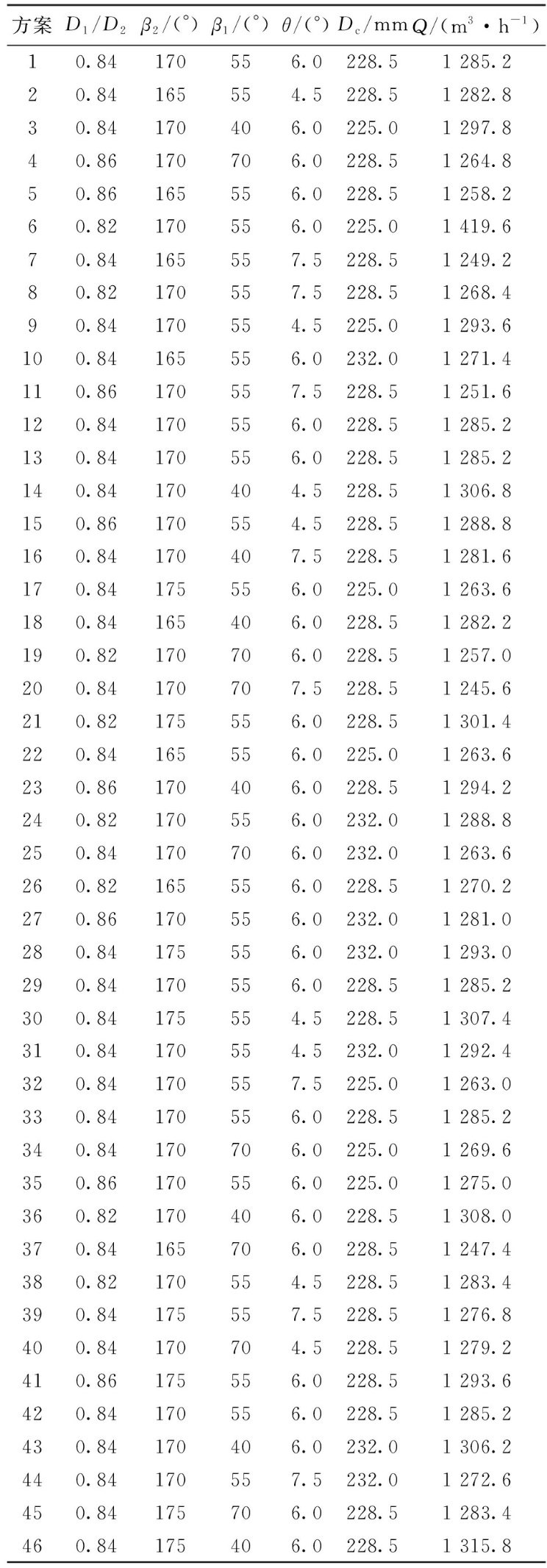
2.2 试验结果 数值模拟采用的计算方法与原型机相同,各试验方案以风量最大的工况点作为数值模拟工况点,通过Box-Behnken试验设计方法得出的设计方案和数值计算结果如表3所示,共46组试验样本空间。获取每组试验的响应计算结果后, 对试验设计 表3 试验设计方案及结果 Table 3 Experimental design scheme and results
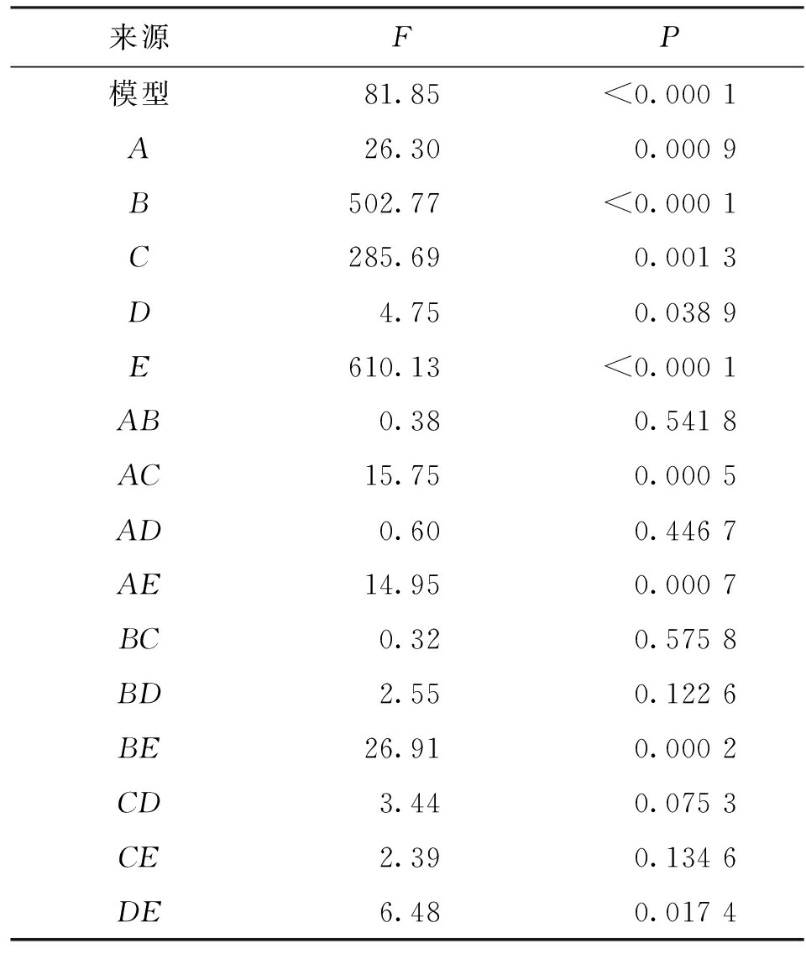
方案进行显著性分析,通过方差分析可获得模型及各项的F值和P值。F值为组间平方和和组内平方和之比,代表显著性差异的水平,若F值大于选定显著性水平下的理论F值,即可认为该项对响应影响显著;P值表示交互作用项的影响重要性,选取显著性水平为0.05,P值小于0.05可认为该因子对响应有显著性影响。F值和P值的计算结果见表4,方差分析的结果显示叶片进口角、叶片出口角对多翼离心风机的风量影响最为显著,其次是叶片中心角,叶轮内外径比和拱点圆直径对风量的影响最小,对于两因子的交互效应来说,β1-β2交互效应对风量的影响效果最为显著,D1/D2-θ和D1/D2-β2的影响次之,其余因子交互效应的显著性不明显。采用最小二乘法进行回归方程的二次多项式拟合,得到基于上述因子的回归方程,如下式所示 Q=46.228-46.166A+0.005 4B- 0.000 013 9C+0.020 5D-0.235E+0.003AB+ 0.006 25AC-0.062 5AD+0.166AE+ 0.000 002 67BC+0.000 036 7BD+ 0.000 103BE-0.000 033CD-0.000 023 5CE+ 0.000 17DE+4.49A2-0.000 091B2- 0.000 004 7C2-0.001 23D2+0.000 17E2 (3) 使用决定系数R2对回归方程进行失拟性检测,当R2越接近1时表示方程越精确, 回归拟合效 表4 试验设计结果的F值和P值 Table 4
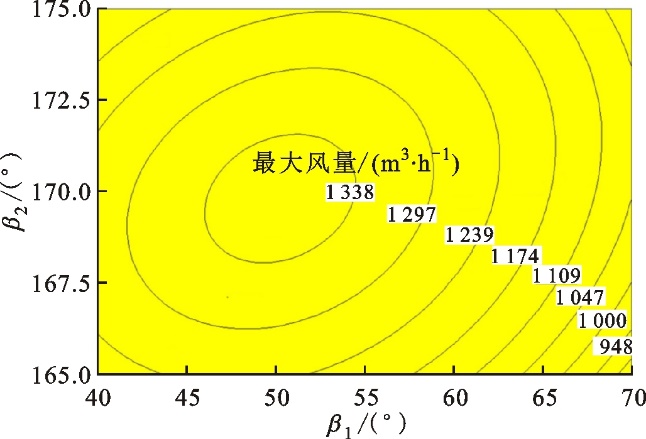
果越好。经过分析,该方程显著性明显,R2为0.985,失拟性不显著,可用来进行响应面优化。根据因子对响应的影响程度以及单因子分析,将相对不显著因子固定为风量最大时因子的最佳值,其中内外径比为0.832,中心角为5.5°,拱点圆半径为232 mm。在此基础上,确定模型中的待定系数叶片出口角与叶片进口角对响应的影响。图9为通过回归方程(4)得到的两因子响应曲面等高线图,在因子的取值范围内存在响应的最佳值,对回归方程最优化求解,得到的双圆弧叶片最优参数分别为:D1=208 mm,D2=250 mm,β1=48°,β2=169°,Dc=232 mm,θ=5.5°。
图9 响应曲面等高线图Fig.9 Response surface contour map
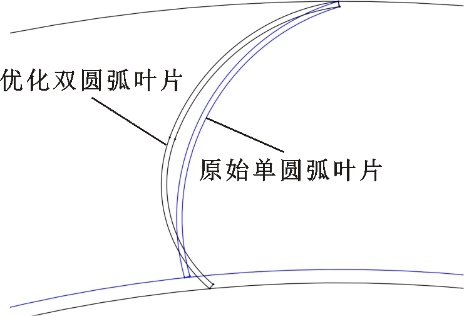
图10 RSM优化叶片与原始叶片Fig.10 RSM optimized blade and original blade 3 叶片优化结果分析 3.1 优化叶片的验证应用 RSM模型在0 Pa静压工况下所预测的双圆弧叶片风机风量为1 343 m3·h-1,计算结果为1 364 m3·h-1,相对误差为1.61%,RSM预测风量与CFD结果较一致,因此RSM预测精度较高。图10为原型叶片截面与RSM优化叶片截面的对比,两者在形状上的主要差别在于β1、β2以及叶片的拱度。在上述回归方程风机性能预测与数值计算的基础上,对RSM双圆弧叶片进行制作,所获得的原型叶轮和优化叶轮的叶间流道如图11所示,相比于原始叶轮逐渐收缩的叶间流道,优化叶轮的叶间流道从进口到出口呈现先略微扩张再逐渐收缩的特点。
(a)原始叶轮 (b)优化叶轮图11 RSM优化叶轮与原始叶轮叶间流道Fig.11 Flow channels of optimized impeller and original impeller 3.2 数值计算结果
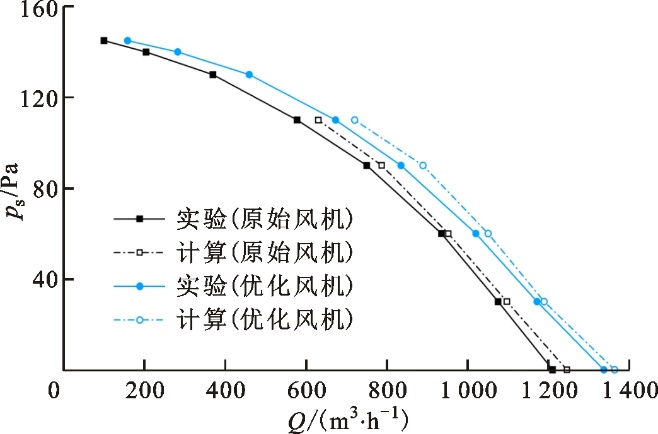
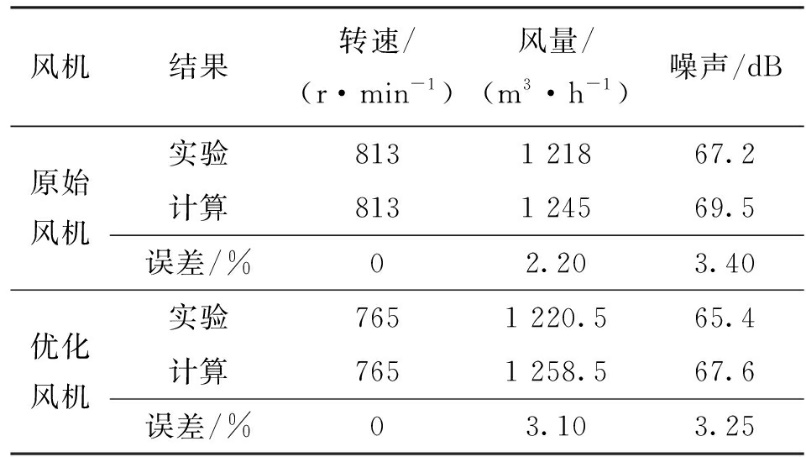
图12 原始风机与优化风机的性能曲线Fig.12 Performance curves of original fan and optimized fan 在相同的叶轮转速下,分别对原型风机与优化风机进行不同工况下的数值计算和风机气动性能试验,结果如图12所示。两风机的数值计算结果与实验测试结果呈相同的变化趋势,并且数值计算的结果均高于实验值。在不同的工况下,两风机的风量计算值与实验值吻合较好,在低出口静压工况下数值计算的误差较小,误差在3%以内。在较高出口静压的工况下,数值计算的误差相对较大,但均在工程要求误差所允许的范围内,考虑到试验过程中的测量误差等因素,可认为本文数值计算模型具有较高准确性。在全工况范围内,优化风机的性能均优于原始风机,这说明与原型风机相比,RSM优化后的双圆弧叶片的气动性能在全工况范围内均提升。在0 Pa出口静压工况下,优化风机的实验风量提升118 m3·h-1,相对提升9.7%。 在0 Pa出口静压工况下降低优化风机的转速,使两风机的风量保持基本相同,并分别测量与计算该状态下的两台风机的噪声,测试结果与数值计算结果如表5所示。在风量相同的状态下,优化风机的转速为767 r·min-1,优化风机功率相对原始风机降低4.7%,原始风机的实验测量噪声为67.2 dB,优化风机的实验测量噪声为65.4 dB,降低了1.8 dB。数值计算与实验的噪声相一致,原型风机和优化风机噪声的计算值与实验值的相对误差分别为3.4%和3.25%,误差较小,进一步说明了计算模型准确性较高,可以用来预测风机的气动特性与噪声。 表5 风机噪声数值计算与实验结果 Table 5 Numerical and experimental results of fan noise
3.3 流场分析
(a)15%叶轮宽度截面
(b)50%叶轮宽度截面
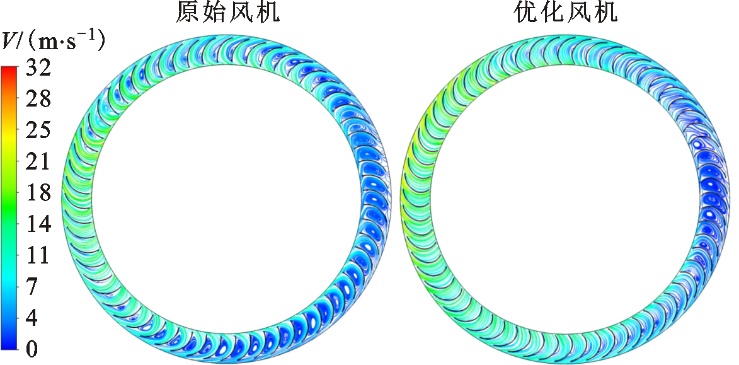
(c)85%叶轮宽度截面图13 不同截面上叶间流道流线Fig.13 Streamlines of inter-blade channel in different cross-sections 选取p-Q曲线中0 Pa静压工况下的两风机内部流场进行分析,揭示RSM优化叶片风机气动性能提升的原因。图13为叶轮宽度方向不同截面上叶间流道的流线图,15%叶轮宽度截面为靠近主进风口侧截面,50%叶轮宽度截面为靠近中盘位置处截面,85%叶轮宽度截面为靠近副进风口位置处截面。不同的叶轮高度截面上叶间流道内的流动分离程度不同,在风机的主进风口处旋涡区域最大,流动分离程度最为严重。原始风机在中盘处的流动分离程度最弱,而优化风机在副进风口侧的流动分离程度最弱,使得副进风口侧风机的做功能力增强。在相同的叶轮截面处,优化风机叶间流道内的旋涡强度均相对原型风机得到大幅改善,叶片压力面的流动分离程度得到明显降低,在副进风口附近叶间流道内的旋涡几乎消失,宏观表现为叶片的做功能力更强,这是由于优化后双圆弧叶片的进、出口角更符合叶轮区域气流进入叶轮的流动角,叶片中弧线的曲线特征对气流有更好的引导和做功作用,使得叶间流道内的速度分布更加均匀,抑制了叶道内的轴向旋涡的产生与发展,进而减小了叶轮内部的局部能量损失和涡流噪声。 图14为50%叶轮宽度截面及蜗舌区域湍动能分布情况,与原始风机内部的湍流脉动状况相比,优化风机在叶片进口区域、风机出口扩压段以及蜗舌区域的强湍动能区域均得到有效抑制并消失,叶间流道内部的低湍动能区域的湍流脉动情况也相对得到缓解,因此湍流脉动所导致的蜗舌和叶片表面的压力脉动减小,宏观表现为蜗舌和叶片工作面宽频噪声的降低。通过RSM方法优化的叶片型线使风机内部的流动状况得到有效改善,减弱了流动紊乱程度,降低了风机内部能量损失。
(a)原始风机 (b)优化风机图14 风机内部湍动能云图Fig.14 Turbulent kinetic energy contour inside the fan 叶轮区域涡量分布如图15所示,两叶轮的高涡量区域基本分布在靠近蜗舌处的叶间流道内,与原型叶轮相比,优化叶轮的高涡量区基本消失,在叶间流道内的涡量均相对原型叶轮减小。这表明优化叶轮的叶片型线可以使气流可以更好地附着叶片表面,有利于流体流动的稳定性,减小湍流边界层所导致叶片表面的压力脉动,缓解叶轮的宽频噪声。
(a)原始风机 (b)优化风机图15 叶轮区域涡量云图Fig.15 Vorticity contour in impeller area 图16为两风机叶轮区域的涡核心区分布,可以看出,优化叶轮相比于原型叶轮在靠近蜗壳出口区域的涡核脱落明显。结合叶轮区域的速度分布,该区域较大的速度使得叶片出口边气流紊乱程度以及与蜗壳壁面的非定常相互作用增强,从而使得该处的涡脱落明显,但由于距离蜗壳壁面较远,该处涡核脱落对风机噪声的影响相对较小。优化叶轮在蜗舌区域及其附近的涡脱落相比原始风机明显减少、变薄,该处距离蜗壳壁面较近,对噪声的贡献较大。根据涡声理论,声波的产生同流体中的旋涡、势流、流体与固体的非定常作用以及旋涡之间的相互作用有密切关系[15],蜗舌及其附近叶轮区域的涡脱落减少表明该处叶轮及蜗壳区域噪声降低。
(a)原始风机 (b)优化风机图16 叶轮区域涡核心区分布Fig.16 Vortex core region distribution in impeller area 3.4 噪声分析 采用1/3倍频程频谱对噪声进行分析,以此来体现多翼离心风机噪声的宽频特性和特定频率范围内风机噪声源的整体能量水平[16-17]。原型风机与RSM优化风机的1/3倍频程频谱如图17所示,优化叶轮的风机在大部分频率范围的声压级相对原型风机有所降低,在1~3 kHz频段范围内的降噪效果最为明显,声压级降低了1.2~2.6 dB。这与图13~图16中原型风机和优化风机内部流场中流动分离、涡分布和涡脱落机理是一致的。优化风机的声压级在风机频谱范围上的分布特性反映了风机内部宽频噪声的降低,结合流场分析,表明采用优化叶片对于叶片前缘气流冲击、叶间流道流动分离以及叶片尾缘涡脱落所引起的涡流噪声有明显的抑制作用。
图17 声压级1/3倍频频谱Fig.17 1/3 octave spectrum of sound pressure level 蜗壳和叶轮壁面静压的变化是风机噪声产生的源头,通过壁面的声压脉动时均值可以直接反映声源强度分布和噪声出现的位置[18]。声压脉动时均值是采样点的静态压力p对时间t偏导的均方根值[19]。原型叶轮与优化叶轮的叶片表面声压脉动时均分布如图18所示,可以看出原型叶轮与优化叶轮的高声压脉动时均区域主要分布在叶片前缘和叶片尾缘,因此叶片前缘和叶片尾缘是叶轮的主要声源位置。在风机做功过程中,进口气流方向在叶片前缘处由轴向转为径向,通过叶片前缘进入叶间流道,使得叶片前缘所受到的气流冲击较大,从而产生噪声。经轴向转径向进入叶片前缘时气流存在一个气流进口冲角,当该冲角与叶片进口角一致时,气流对叶片前缘的冲击较小,可以更加平稳地进入叶间流道。根据图18,原始叶轮的叶片前缘的高声压脉动时均区域较大,而优化叶轮的叶片前缘的声压脉动时均区域几乎消失,仅仅存在叶片厚度面上的小范围区域。这是由于原始叶片的进口角高于气流进口冲角,使得气流对叶片前缘的冲击较大,产生较大的噪声,而优化叶片的进口角与气流进口冲角一致,使得气流冲击所引起的叶片前缘声压脉动明显减少,从而有效降低了叶片前缘所引起的涡流噪声。结合图13中叶间流道流线图可以看出,合适的叶片进口角不仅可以降低叶片前缘压力脉动所产生的噪声,还可以使气流更加平稳地进入叶间流道,减小叶片背面所产生的脱流旋涡,进一步降低叶间流道流动分离所产生的边界层噪声。叶片尾缘区域的声压时均脉动较高,是由于叶片出口角的不合理对气流的阻碍以及叶片出口高速气流与蜗壳内壁的冲击,造成气流持续产生不规则局部压力脉动反作用于叶片。图18显示优化叶片的尾缘区域的声压脉动强度明显减弱,较大声压时均脉动区域的分布面积也减小。这是由于优化叶轮合理的叶间流道使叶片尾缘的尾迹分离涡脱落程度改善,以及优化叶片合适的出口角使得出口高速气流与蜗壳近处内壁的冲击作用得到缓解,从而使得叶片尾缘区域噪声的强度降低。
(a)原始风机 (b)优化风机图18 叶轮表面声压脉动分布Fig.18 Distribution of sound pressure pulsation on impeller 图19为原始风机与优化风机蜗壳及蜗舌区域的声压脉动时均分布,原型风机与优化风机的声压脉动区域主要分布在蜗壳弧形壁面和蜗舌区域,是主要的气动噪声源,其中蜗舌区域的声压时均脉动强度较大,对噪声的贡献也较大。蜗壳壁面上的声压时均脉动产生的原因主要是叶片尾迹流与蜗壳的非定常相互作用,优化风机在蜗壳壁面上的声压时均脉动较原型风机得到明显改善。这是由于优化风机叶片所产生的尾迹分离涡与蜗壳壁面的非定常相互作用小,进一步是说明了优化叶片具有更合适的叶片出口角的结论。蜗舌区域压时均脉动强度高的原因是叶片旋转产生的尾流与蜗舌周期性干涉作用较强,因此蜗舌区域是主要的离散噪声源。优化风机蜗舌区域的声源区域面积及声压脉动强度均低于原型风机,这是由于优化后叶片旋转所形成的流场更加均匀,尾流与蜗舌的周期性干涉作用减弱,从而降低了叶片周期性旋转所产生的离散噪声。
(a)原始风机 (b)优化风机图19 蜗壳表面声压脉动分布Fig.19 Distribution of sound pressure pulsation on volute 4 结 论 本研究采用数值计算、RSM寻优设计及实验测量相结合的方法,对多翼离心风机的双圆弧叶片进行参数化设计及优化,探究双圆弧叶片设计对风机气动性能和噪声的影响程度,获得的主要结论如下。 (1)基于RSM和CFD方法得到了双圆弧叶片的最优参数组合及各参数对响应的影响程度,其中叶片进口角和出口角对风量影响最为显著,拱点圆直径对风量的影响最小。对于两因子的交互效应来说,叶片进口角与叶片出口角的交互效应对风量的影响效果最为显著。 (2)实验与数值结果均表明优化的双圆弧叶片多翼离心风机的气动性能得到提升。在相同转速下,优化风机的风量较原型提升了9.7%;在相同风量下,优化风机的功率相对降低了4.7%,噪声降低了1.8 dB。 (3)流场及声场的可视化分析表明,优化叶片型线的流动阻力更小,叶间流道的流速分布更加均匀。叶片进口角与进口气流冲角的一致性使得叶片前缘气流冲击所引起声压脉动有效减小;叶片的双圆弧曲线特征使得叶片背面脱流旋涡和流动分离程度减弱,使得叶片前缘的来流冲击噪声和叶间流道紊流边界层噪声降低。优化后的叶片出口角改善了叶片出口尾迹涡脱落程度和叶片出口流动状态,抑制了叶片出口周期性尾流与蜗舌的非定常相互作用,从而降低了叶片尾迹涡引起的宽频噪声和叶片周期性旋转产生的离散噪声。 参考文献: [1]赵燕杰, 谭俊飞, 党飞龙, 等. 离心风机集流器的响应面优化设计 [J]. 西安交通大学学报, 2015, 49(11): 49-54. ZHAO Yanjie, TAN Junfei, DANG Feilong, et al. Optimization design of centrifugal fan inlet collector by response surface methodology [J]. Journal of Xi’an Jiaotong University, 2015, 49(11): 49-54. [2]秦国良. 多翼离心通风机变安装角性能计算 [J]. 风机技术, 1999(1): 21-22, 28. QIN Guoliang. Calculation of variable installation angle performance of multi-blade centrifugal fan [J]. Chinese Journal of Turbomachinery, 1999(1): 21-22, 28. [3]ADACHI T, SUGITA N, YAMADA Y. Study on the performance of a sirocco fan (optimum design of blade shape) [J]. International Journal of Rotating Machinery, 2001, 7(6): 405-414. [4]李淼, 赵军. 小型多翼离心风机叶片斜切分析及试验研究 [J]. 风机技术, 2012(4): 9-12, 17. LI Miao, ZHAO Jun. Research on beveling impellers in a miniature forward-curved multi-blade centrifugal fan and performance tests [J]. Chinese Journal of Turbomachinery, 2012(4): 9-12, 17. [5]WANG Ke, JU Yaping, ZHANG Chuhua. Experimental and numerical investigations on effect of blade trimming on aerodynamic performance of squirrel cage fan [J]. International Journal of Mechanical Sciences, 2020, 177: 105579. [6]熊仲营, 王梦豪, 刘小民, 等. 采用仿鱼形叶片的多翼离心风机性能研究 [J]. 西安交通大学学报, 2018, 52(11): 22-29. XIONG Zhongying, WANG Menghao, LIU Xiaomin, et al. Study on the aerodynamic performance of multi-blade centrifugal fan with bionic blades inspired by carangiform fish [J]. Journal of Xi’an Jiaotong University, 2018, 52(11): 22-29. [7]王梦豪, 吴立明, 刘小民, 等. 采用仿鸮翼叶片降低空调用离心风机气动噪声的研究 [J]. 西安交通大学学报, 2018, 52(6): 55-61. WANG Menghao, WU Liming, LIU Xiaomin, et al. A study on noise reduction of centrifugal fan in air conditioner by using the bionic blade inspired by the owl wing [J]. Journal of Xi’an Jiaotong University, 2018, 52(6): 55-61. [8]刘小民, 汤虎, 王星, 等. 苍鹰翼尾缘结构的单元仿生叶片降噪机理研究 [J]. 西安交通大学学报, 2012, 46(1): 35-41. LIU Xiaomin, TANG Hu, WANG Xing, et al. Noise-reduction mechanism of bionic coupling blade based on the trailing edge of goshawk wing [J]. Journal of Xi’an Jiaotong University, 2012, 46(1): 35-41. [9]何立博, 姜涛, 李志峰, 等. 多翼离心风机叶轮的正交设计与试验分析 [J]. 流体机械, 2016, 44(9): 7-11, 30. HE Libo, JIANG Tao, LI Zhifeng, et al. Orthogonal design and experiment analysis of multi-blades centrifugal fan impeller [J]. Fluid Machinery, 2016, 44(9): 7-11, 30. [10]李云龙, 郭朋华, 何立博, 等. 油烟机内多翼离心风机的响应面优化设计 [J]. 工程热物理学报, 2018, 39(5): 1056-1062. LI Yunlong, GUO Penghua, HE Libo, et al. Optimization of squirrel-cage fan in range hood based on response surface methodology [J]. Journal of Engineering Thermophysics, 2018, 39(5): 1056-1062. [11]肖千豪, 王军, 蒋博彦, 等. 多翼离心风机叶片参数化及多目标优化研究 [J]. 工程热物理学报, 2020, 41(12): 2977-2981. XIAO Qianhao, WANG Jun, JIANG Boyan, et al. Parametric and multi-objective optimization of the squirrel cage fan [J]. Journal of Engineering Thermophysics, 2020, 41(12): 2977-2981. [12]王湛. 双圆弧叶片多翼风机内流场的数值模拟及叶型研究 [D]. 济南: 山东大学, 2007: 14-30. [13]王珂, 琚亚平, 张楚华. 基于分组模型及仿生蜗舌的多翼离心风机设计 [J]. 工程热物理学报, 2017, 38(8): 1671-1675. WANG Ke, JU Yaping, ZHANG Chuhua. Design of multi-blade centrifugal fan based on grouping model and bionic volute tongue [J]. Journal of Engineering Thermophysics, 2017, 38(8): 1671-1675. [14]GALLAGHER E, O’BRIEN C M, SCANNELL A G M, et al. Use of response surface methodology to produce functional short dough biscuits [J]. Journal of Food Engineering, 2003, 56(2/3): 269-271. [15]LI Dian, LIU Xiaomin, HU Fujia, et al. Effect of trailing-edge serrations on noise reduction in a coupled bionic aerofoil inspired by barn owls [J]. Bioinspiration & Biomimetics, 2020, 15(1): 016009. [16]PREZELJ J, NOVAKOVI [17]王雷, 刘小民, 刘刚, 等. 轴流风机仿生耦合叶片降噪机理研究 [J]. 西安交通大学学报, 2020, 54(11): 81-90. WANG Lei, LIU Xiaomin, LIU Gang, et al. Noise reduction mechanism of bionic coupled blades of axial flow fan [J]. Journal of Xi’an Jiaotong University, 2020, 54(11): 81-90. [18]WU Liming, LIU Xiaomin, WANG Menghao. Effects of bionic volute tongue on aerodynamic performance and noise characteristics of centrifugal fan used in the air-conditioner [J]. Journal of Bionic Engineering, 2020, 17(4): 780-792. [19]LI Dian, LIU Xiaomin. A comparative study on aerodynamic performance and noise characteristics of two kinds of long-eared owl wing models [J]. Journal of Mechanical Science and Technology, 2017, 31(8): 3821-3830. 窗体顶端 窗体底端 Parametric Optimization Design of Double-Circular Arc Blade Used in Multi-Blade Centrifugal Fan and Its Aerodynamic Analysis WANG Jiahao1,LIU Xiaomin1,TIAN Chenye1,QIAO Yang1,WANG Yue1, XI Guang1,GONG Dongqiao2 (1. School of Energy and Power Engineering, Xi’an Jiaotong University, Xi’an 710049, China; 2. Qingdao Haier Technology R&D Co. Ltd., Qingdao, Shandong 266000, China) Abstract:In order to improve the aerodynamic performance and noise characteristics of multi-blade centrifugal fan, combining with the characteristics of high degree of freedom in the design of inter-blade flow channel of double-arc blade and based on a single-arc blade multi-blade centrifugal fan with better performance, a full parameter matching optimization design of double-arc blade is carried out through the combination of CFD and experiments. Taking the air volume of the fan under 0 Pa static pressure condition as the optimization goal, the Box-Behnken response surface experimental design method is used to determine the inlet angle, outlet angle, inner to outer diameter ratio, arch point diameter and central angle for parameter design, and 46 sets of sample spaces are obtained. Through the quadratic regression fitting of the design parameters and the sample results, the functional relationship between the parameters of the double-arc blade and the air volume, as well as the optimal parameter combination, is obtained. The results show that the inlet angle and outlet angle have the highest sensitivity to the air volume in all main effects, while the inlet angle, the outlet angle, the inner diameter to outer diameter ratio and the central angle have the highest sensitivity to air volume in all interaction effects. The CFD and FW-H methods are used to calculate the aerodynamic performance and sound field characteristics of the optimized double-arc blade fan and the prototype fan. The results show that the air volume of the optimized fan increases by 118 m3·h-1 Keywords:multi-blade centrifugal fan; double-arc blade; Box-Behnken RSM; parametric design; aerodynamic performance 收稿日期:2021-06-26。 作者简介:王加浩(1995—),男,博士生;刘小民(通信作者),男,教授,博士生导师。 基金项目:国家重点研发计划资助项目(2019YFB1504601)。 网络出版时间:2021-10-25 网络出版地址:http:∥kns.cnki.net/kcms/detail/61.1069.T.20211021.1525.002.htm |